深度学习引言

什么是神经网络

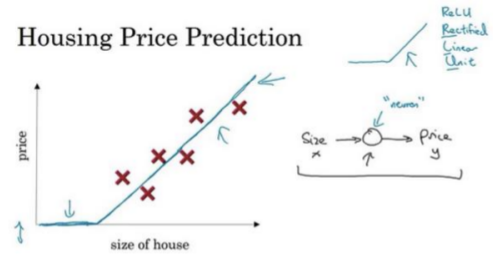
简单神经网络引子
上图说明了最简的神经网络，小圆圈表示一个单独的神经元，连接你的网络实现左边图的功能。稍微大点的神经网络如下图所示。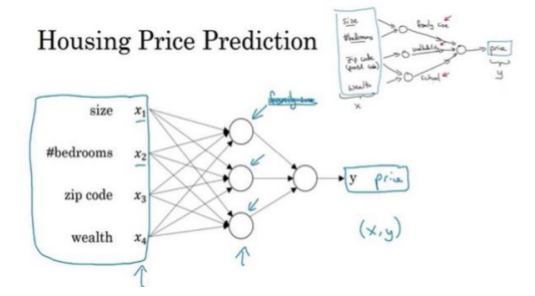
稍微大点神经网络
当实现它之后,要做的只是输入x，就能得到输出y。因为它可以自己计算训练集中样本的数目以及所有的中间过程。

结构化数据和非结构化数据

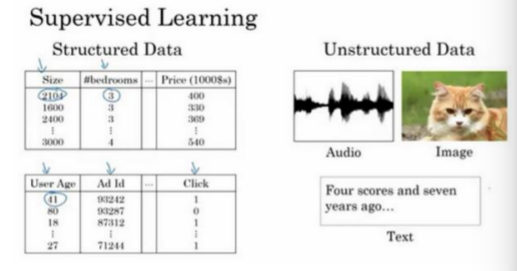
结构化数据意思是每个特征，比如说房屋大小、卧室数量，或者是一个用户的年龄，都有一个很好的定义。例如在房价预测中，可能有一个数据库，有专门的几列数据说明卧室的大小和数量，这就是结构化数据。或预测用户是否会点击广告，可能会得到关于用户的信息，比如年龄以及关于广告的一些信息，然后对预测分类标注，这就是结构化数据。
非结构化数据是指比如音频或者你想要识别的图像或文本中的内容。这里的特征可能是图像中的像素值或文本中的单个单词。

深度学习兴起的原因

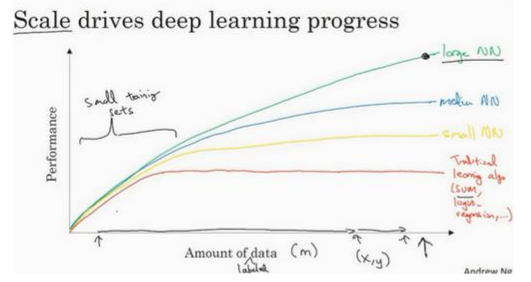规模驱动深度学习事实上，在神经网络上获得更好的性能的可靠方法是要么训练一个更大的神经网络，要么投入更多的数据，这只能在一定程度上起作用，因为最终会耗尽数据，或者最终网络规模很大导致花费很长时间去训练。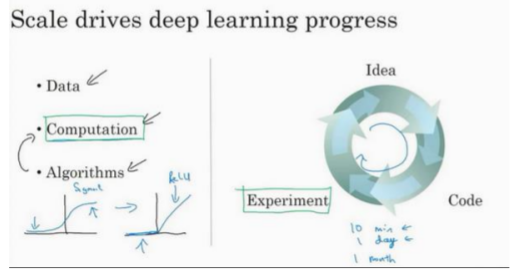深度学习兴起总结

许多算法的创新都在尝试使神经网络跑得更快，一个例子如下图（激活函数的改变）。
使用sigmoid函数问题是，在横坐标值很大或很小区域，sigmoid函数的梯度会接近零，学习的速度会变得非常缓慢，当实现梯度下降以及梯度接近零的时候，参数会更新的很慢，所以学习的速率会变的很慢，通过改变激活函数为ReLU的函数(修正线性单元)，ReLU的梯度对于所有输入的负值都是零，因此梯度不会趋向逐渐减少到零。通过将Sigmod函数转换成ReLU函数，能够使得梯度下降(gradient descent)算法运行的更快。

神经网络编程基础

实现神经网络的时候，通常不使用for循环遍历整个训练集（使用向量化的手段实现）。
神经网络的计算中，通常先有前向传播(foward propagation)步骤，接着有反向传播(backward propagation)步骤。

logistic回归

以logistic regression为基础，来引入神经网络。logistic regression是一个用于处理二分类(binary classification)的算法。logistic regression使用的参数如下：

输入特征向量：$x\in R^{n_x}$，其中$n_x$表示特征向量的维数
样本标签：$y\in \{0,1\}$
权重：$w\in R^{n_x}$
偏置：$b\in R$
输出：$\widehat {y}=\sigma(w^Tx+b)$，其中$\sigma$是Sigmoid函数

logistic regression可以看成一个很小的神经网络，例子如下图所示。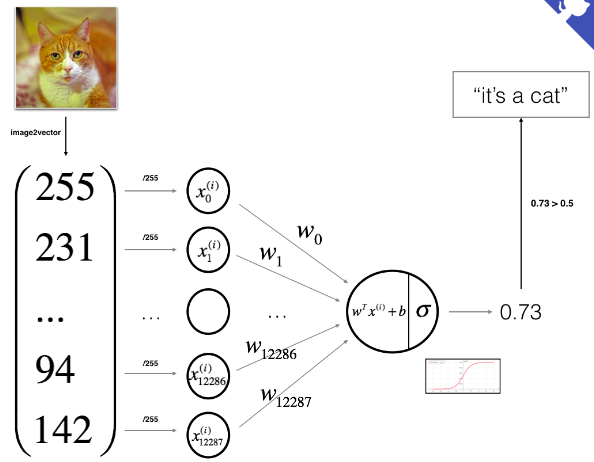 logistic 回归例子

下面给出相关符号定义：
x:表示一个$n_x$维数据，为输入，维度为$(n_x,1)$
y:表示输出结果，取值为$(0,1)$
$(x^{(i)},y^{(i)})$:表示第$i$组数据
$X=[x^{(1)},x^{(2)},\ldots ,x^{(m)}]$:表示数据集的所有输入值，$X$为$n_x \times m$的矩阵，其中$m$表示样本数目（样本横着放）
$Y=[y^{(1)},y^{(2)},\ldots ,y^{(m)}]$:表示数据集的所有输出值，维度为$1\times m$(样本横着放）

代价函数(Cost Function)

通过训练代价函数来得到logistic regression的参数$w$与$b$

损失函数用来衡量输出值和实际值的接近程度，一般情况损失函数定义为平方差损失，如下：$$L(\widehat {y},y)=\dfrac{1}{2}(\widehat y -y)^2$$但logistic回归不这么做，因为之后的优化目标变为非凸的，梯度下降法可能找不到全局最优。
logistic回归的损失函数一般用$$L(\widehat {y},y)=-(y\log{\widehat y})-(1-y)\log{(1-\widehat y)}$$损失函数是在单个训练样本中定义，衡量算法在单个训练样本中表现如何。代价函数衡量算法在全部训练样本上的表现，是对$m$个样本损失函数求和并除以$m$，公式如下$$J(w,b)=\dfrac{1}{m}\sum_{i=1}^{m}L(\widehat {y}^{(i)},y^{(i)})=\dfrac{1}{m}\sum_{i=1}^{m}\Big(-y^{(i)}\log{\widehat {y}^{(i)}}-(1-y^{(i)})\log(1-\widehat {y}^{(i)})\Big)$$可以通过极大似然推导。

梯度下降法

梯度：函数在某一点的梯度是这样一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。沿梯度方向，函数值增加最快（此时方向导数是正值，取最大）。

模型的训练目标是找到合适的参数$w$与$b$以最小化代价函数，为便于演示，假设参数都是一维的，可以得到如下参数$w$与$b$和代价函数$J$的关系图: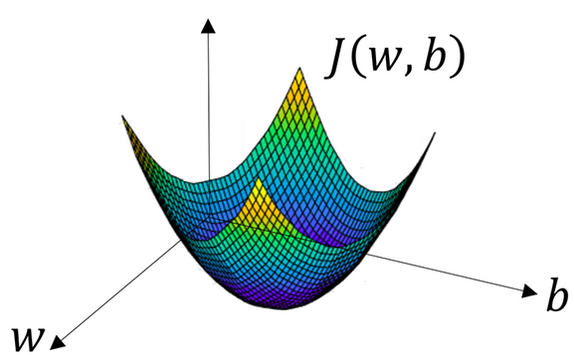 代价函数图代价函数J是一个凸函数，有一个全局最低点（无论如何选择初始值，都可找到最优值）。
参数$w$的更新公式为$$w:=w-\alpha\dfrac{\partial {J(w,b)}}{\partial w}$$参数$b$的更新公式$$b:=b-\alpha\dfrac{\partial {J(w,b)}}{\partial b}$$其中$\alpha$表示学习率，即每次更新$w$的步长。

计算图

神经网络中的计算是由多个计算网络输出的前向传播与计算梯度的后向传播构成。所谓的反向传播也就是计算梯度，用于更新参数的。计算图例子如下: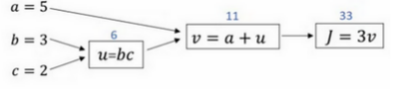

Logistic 回归的梯度下降法

假设输入的特征向量是$2$维的，则输入参数共有$x_1$，$x_2$，$w_1$，$w_2$，$b$五个参数，得到其计算图如下: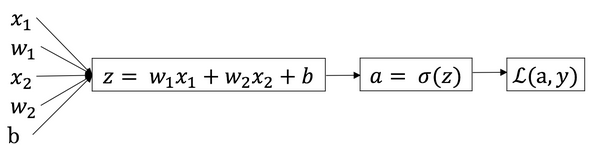 logistic 计算图首先反向求出$L$对$a$的倒数:$$da=\dfrac{dL(a,y)}{da}=-\dfrac{y}{a}+\dfrac{1-y}{1-a}$$继续反向求出$L$对$z$的导数:$$dz=\dfrac{dL}{dz}=\dfrac{dL}{da}\dfrac{da}{dz}=a-y$$类似反向传播可以求出损失函数$L$对参数$w_1$，$w_2$，$b$的导数。根据如下公式对参数更新:$$w_1:=w_1-\alpha dw_1$$$$w_2:=w_2-\alpha dw_2$$$$b:=b-\alpha db$$开始将单个样本拓展到整个训练集的代价函数，如下：$$J(w,b)=\dfrac{1}{m}\sum_{i=1}^{m}L(\widehat {y}^{(i)},y^{(i)})$$$$a^{(i)}=\widehat {y}^{(i)}=\sigma (z^{(i)})=\sigma (w^{T}x^{(i)}+b)$$对其中的某个参数求导（其他类似）：$$\dfrac{dJ(w,b)}{dw_1}=\dfrac{1}{m}\sum_{i=1}^{m}\dfrac{dL(a^{(i)},y^{(i)})}{dw_1}$$下面给出完整的Logistic回归的训练流程（假设输入特征为二维）: logistic 回归流程图以上完成梯度下降的一次迭代。
上述的流畅图的效率较低，因为需要编写两个for循环（第一个循环$m$个样本，第二个循环$n$个特征）。向量化可以显示解决for循环效率低的问题。

向量化

经验法则：编写代码，只要有其他可能就不要使用for循环，比如可以考虑向量化

杂谈：向量化与for循环效率对比:

import numpy as np
import time

a = np.random.rand(1000000)
b = np.random.rand(1000000)
tic = time.time()
c = np.dot(a,b)
toc = time.time()
print(c)
print('Vectorized version: ' + str((toc-tic)*1000) + 'ms')

c=0
tic = time.time()
for i in range(1000000):
    c += a[i] * b[i]
toc = time.time()
print(c)
print('For loop: ' + str((toc-tic)*1000) + 'ms')

结果:

250235.98496807975
Vectorized version: 1.1947154998779297ms
250235.98496807023
For loop: 445.22929191589355ms
可以说是差距巨大。

回到Logistic回归上，其向量化版本的流程如下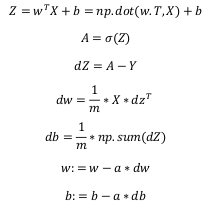：向量化版本注意：上述只是完成一次迭代，多次迭代依然需要for循环。

Numpy 中广播(broadcasting)

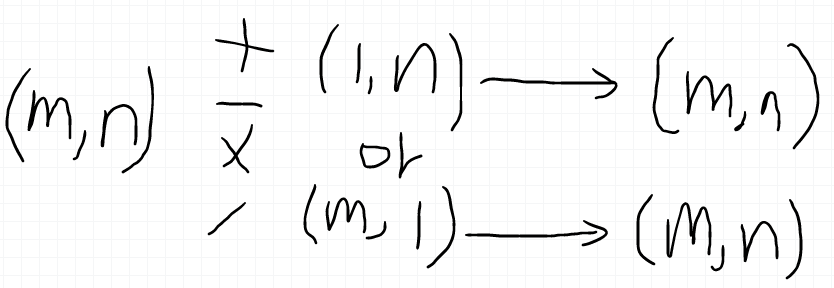详细介绍参考官方文档

编程建议

不要使用形如a.shape=(n,)的向量，而应该使用形如a.shape=(n,1)的向量；
程序中要适当使用assert(a.shape==(n,1))，不要担心效率问题;

浅层神经网络

神经网络表示

神经网络表示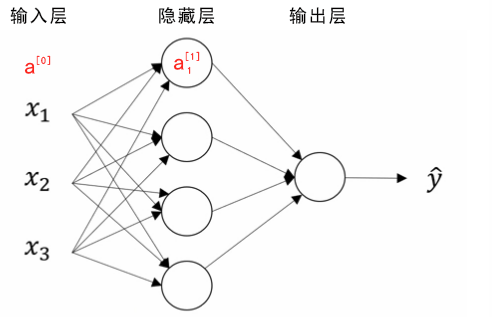竖向堆叠的特征（对应一个样本）称为神经网络的输入层(the input layer)；
隐藏层(hidden layer)的含义指在训练集中，中间节点的真正值无法看到；
输出层(the output layer)负责输出预测值。
上图是一个双层神经网络，也称为单隐层神经网络。一般计算神经网络层数时，不考虑输入层。
下面是约定的符号表示：

输入层的激活值为$a^{[0]}$($a^{[0]}=x)$
隐藏层的激活值为$a^{[1]}$，其中第一个单元（或节点）表示为$a_{1}^{[1]}$，输出层类似。在上图中$$a^{[1]}=\begin{bmatrix} a_{1}^{[1]} \\ a_{2}^{[1]} \\ a_{3}^{[1]} \\ a_{4}^{[1]} \end{bmatrix}$$
隐藏层和输出层都是带有参数$W$与$b$的，使用上标$[i]$表示第$i$层的参数。在上图中$W^{[1]}$是一个$4\times 3$矩阵，$b^{[1]}$是一个$4\times 1$矩阵（因为有$4$个节点，$3$个输入特征）,同理$W^{[2]}$是一个$1\times 4$矩阵，$b^{[2]}$是一个$1\times 1$矩阵

计算神经网络的输出（前向传播）

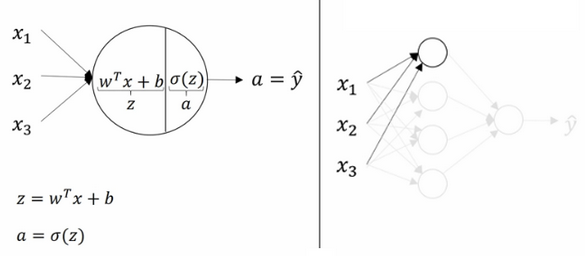神经网络计算神经网络不过是将Logistic回归的计算步骤重复多次。详细的计算结果如下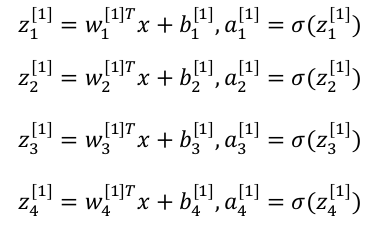神经网络计算结果用向量表示如下$$z^{[1]}=(W^{[1]})a^{[0]}+b^{[1]}$$$$a^{[1]}=\sigma(z^{[1]})$$
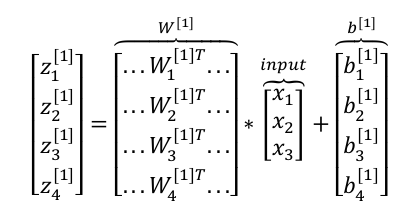其中$$a^{[1]}=\begin{bmatrix} a_{1}^{[1]} \\ a_{2}^{[1]} \\ a_{3}^{[1]} \\ a_{4}^{[1]} \end{bmatrix}$$同理对于输出层有$$z^{[2]}=(W^{[2]})a^{[1]}+b^{[2]}$$$$\widehat y=a^{[2]}=\sigma(z^{[2]})$$以上都是针对单个样本的情况，对于有$m$个样本，向量化的方式如下:
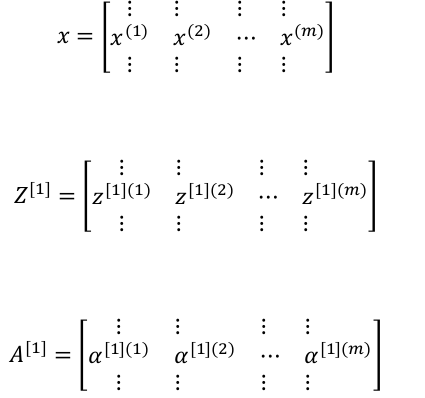多向量表示进而得到如下公式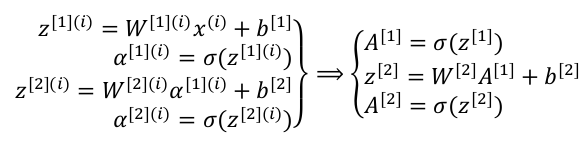向量表示结果

激活函数

之前的激活函数选择都是sigmoid函数，单有时其他的激活函数效果可能会更好。
可选的激活函数有：

tanh函数（双曲正切函数）:$$a=\dfrac{e^z-e^{-z}}{e^z+e^{-z}}$$效果几乎总是比sigmoid函数好（除了二元分类的输出层，因为希望输出结果介于$0$与$1$之间），因为函数输出值介于$-1$与$1$之间，激活函数的平均值接近$0$，有类似数据中心化效果，方便下一层的学习。
但tanh函数和sigmoid函数有一个共同缺点：当$z$很大或很小时，函数梯度趋向于$0$，使得梯度下降算法很慢。
ReLu函数(the rectified linear unit，修正线性单元):$$a=max(0,z)$$当$z>0$时，梯度为$1$提高神经网络基于梯度的算法，编程时，在$z=0$处导数设为$1$或$0$都行。
Leaky ReLu函数（带泄漏的ReLu）:$$a=max(0.01z,z)$$不常用（这里的$0.01$根据实际情况可修改）。

四个激活函数的图形如下: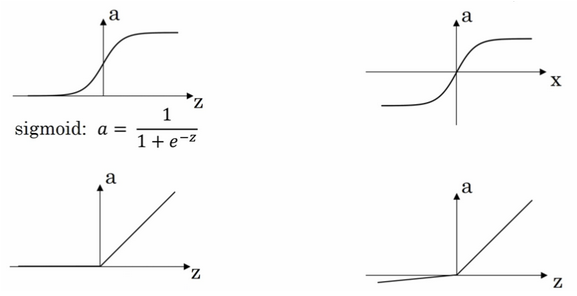 激活函数图形选择激活函数的经验法则是：如果输出值是$0$，$1$值（二分类），则输出层选择sigmoid函数，其他的单元选择ReLu函数。这是很多激活函数的默认选择，如果在隐藏层上不确定选择哪个激活函数，通常选择ReLu函数，有时也选择tanh函数。当然不同的层可以选择不同的激活函数。

使用非线性激活函数的原因

若使用线性激活函数，无论神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，就成了最原始的感知机了。

激活函数的导数

在神经网络使用反向传播时，需要计算激活函数的梯度，这里直接给出之前介绍的激活函数的梯度（导数）。

sigmoid函数:$$a=\dfrac{1}{1+e^{-z}}$$其导数为$a(1-a)$。
tanh函数（双曲正切函数）:$$a=\dfrac{e^z-e^{-z}}{e^z+e^{-z}}$$其导数为$1-a^2$。
ReLu函数(the rectified linear unit，修正线性单元):$$a=max(0,z)$$其导数为$a’=\begin{cases}0,z>0\\ 1,z<0\\ undefine,z=0 \end{cases}$。

神经网络梯度下降法

前向传播（计算输出值）: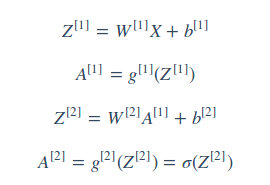
反向传播（计算梯度）:反向梯度下降公式（左）和代码向量化（右）

随机初始化

如果在初始时将两个隐藏神经元的参数设置为相同的大小，那么两个隐藏神经元对输出单元的影响也是相同的，通过反向梯度下降去进行计算的时候，会得到同样的梯度大小，所以在经过多次迭代后，两个隐藏层单位仍然是对称的。无论设置多少个隐藏单元，其最终的影响都是相同的，那么多个隐藏神经元就没有了意义。
初始化时候，参数$W$要进行随机初始化，不可设置为$0$。参数$b$ 因为不存在对称性的问题，可以设置为$0$。
以$2$个输入，$2$个隐藏神经元为例，python代码如下:

1 2	W = numpy.random.rand(2,2)*0.01 b = numpy.zeros((2,1))

注意：这里将$W$的值乘以$0.01$（或者其他的常数值）的原因是为了使得权重$W$初始化为较小的值，这是因为使用sigmoid函数或者tanh函数作为激活函数时，$W$比较小，则$Z=WX+b$ 所得的值趋近于$0$，梯度较大，能够提高算法的更新速度。而如果$W$设置的太大的话，得到的梯度较小，训练过程因此会变得很慢。ReLU和Leaky ReLU作为激活函数时不存在这种问题，因为在大于$0$的时候，梯度均为$1$。

建议

python中numpy.sum()函数有一个keepdims关键字很有用。
编程中要核对网络各层的维数；
遇到新的问题要从单层（例如Logistic回归）到多层（也就是从简单到复杂）。

深层神经网络

深层神经网络符号约定

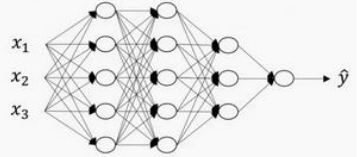深层神经网络 $L$表示层数: 上图中$L=4$，输入层的索引为$0$；
第一个隐藏层$n^{[1]}=5$表示有$5$个隐藏神经元，同理$n^{[2]}=5$，$n^{[3]}=3$，$n^{[4]}=1$。输入层$n^{[0]}=n_x=3$；
$a^{[l]}$表示第$l$层激活后结果；
$W^{[l]}$表示第$l$层计算$Z^{[l]}$的权重，类似$Z^{[l]}$中的$b^{[l]}$也一样。
输入特征为$x$，约定$x=a^{[0]}$。

前向传播和反向传播

前向传播:
输入：$a^{[l-1]}$
输出：$a^{[l]}$，cache($z^{[l]})$，cache($w^{[l]})$，cache($b^{[l]})$
公式：$$z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}$$$$a^{[l]}=g^{[l]}(z^{[l]})$$向量化后的公式$$Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}$$$$A^{[l]}=g^{[l]}(Z^{[l]})$$
反向传播
输入：$da^{[l]}$
输出：$da^{[l-1]}$，$dW^{[l]}$，$db^{[l]}$
公式：深层神经网络反向公式

搭建深层神经网络块

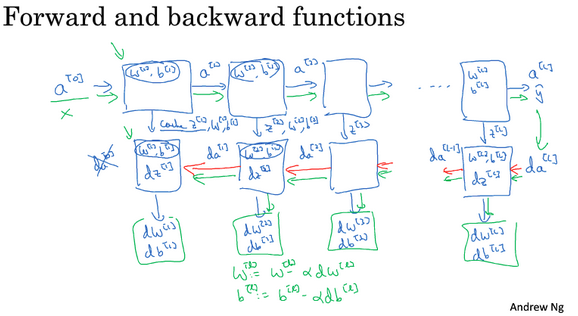深层神经网络反向公式神经网络的一步训练（一个梯度下降循环），包含了从$a^{[0]}$（即$x$）经过一系列正向传播计算得到$\widehat y$（即$a^{[l]}$）。然后计算$da^{[l]}$，开始实现反向传播，得到所有的导数项，$W$和$b$也会在每一层被更新。
在代码实现时，可以将正向传播过程中计算出来的$z$值缓存下来，待到反向传播计算时使用。

网络矩阵维数

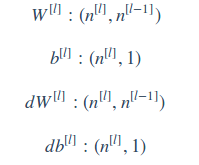矩阵维数在向量化之前有$$z^{[l]},a^{[l]}:(n^{[l]},1)$$在向量化后有$$Z^{[l]},A^{[l]}:(n^{[l]},m)$$计算反向传播时，$dZ$、$dA$与$Z$和$A$维数一样。

使用深层神经网络原因

以人脸识别为例子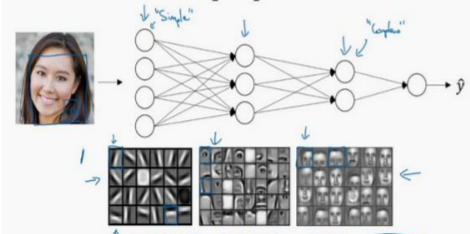对于人脸识别，神经网络的第一层从原始图片中提取人脸的轮廓和边缘，每个神经元学习到不同边缘的信息；网络的第二层将第一层学得的边缘信息组合起来，形成人脸的一些局部的特征，例如眼睛、嘴巴等；后面的几层逐步将上一层的特征组合起来，形成人脸的模样。随着神经网络层数的增加，特征也从原来的边缘逐步扩展为人脸的整体，由整体到局部，由简单到复杂。层数越多，那么模型学习的效果也就越精确。
随着神经网络的深度加深，模型能学习到更加复杂的问题，功能也更加强大。

参数VS超参数

参数即是我们在过程中想要模型学习到的信息（模型自己能计算出来的），例如$W^{[l]}$和$b^{[l]}$等。而超参数（hyper parameters）即为控制参数的输出值的一些网络信息（需要人经验判断）。超参数的改变会导致最终得到的参数$W^{[l]}$和$b^{[l]}$等的改变。
典型的超参数有：

学习速率: $\alpha$
迭代次数: $N$
隐藏层层数: $L$
每一层神经元个数: $n^{[l]}$
激活函数$g(z)$选择

开发新应用时，预先很难准确知道超参数的最优值应该是什么。因此，通常需要尝试很多不同的值。应用深度学习领域是一个很大程度基于经验的过程。