卷积神经网络基础
计算机视觉
计算机视觉 ( Computer Vision )是一个飞速发展的领域,其中深度学习技术起到重要作用。计算机视觉中有许多的应用,例如图片分类 ( Image Classification ) 、目标检测 ( Object detection ) 、图片风格转换 ( Neural Style Transfer ) 等等。
应用计算机视觉时可能要面临的一个挑战是输入的数据可能会非常大。例如输入一张 \(1000\times 1000\times 3 \) 的图片,则神经网络的输入维度将达到 300 万,使得神经网络的权重 \(W\) 的参数非常多,会带来两个后果:
- 难以获得足够数据来防止神经网络发生过拟合;
- 需要很大的内存和计算代价。
因此,需要利用卷积神经网络 ( Convolutional Neural Network, CNN )。
边缘检测
卷积运算 (
Convolutional Operation) 是卷积神经网络最基本的组成部分。(神经网络由浅层到深层,分别可以检测出图片的边缘特征、局部特征(例如眼睛、鼻子等)、到最后一层可由前面检测的特征识别整体面部轮廓。)
图片常做的边缘检测有垂直边缘检测和水平边缘检测等,如下图所示。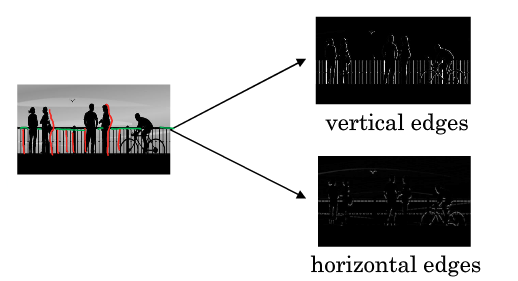 图片的边缘检测可以通过与相应滤波器卷积来实现。例如在垂直边缘检测中,原始图片是 \(6\times 6 \) ,中间的矩阵称为滤波器 (
图片的边缘检测可以通过与相应滤波器卷积来实现。例如在垂直边缘检测中,原始图片是 \(6\times 6 \) ,中间的矩阵称为滤波器 (filter) ,大小为 \(3\times 3 \) ,卷积后的图片大小为 \(4\times 4\) ,如下图所示(以左上角和右下角为例,数值表示灰度):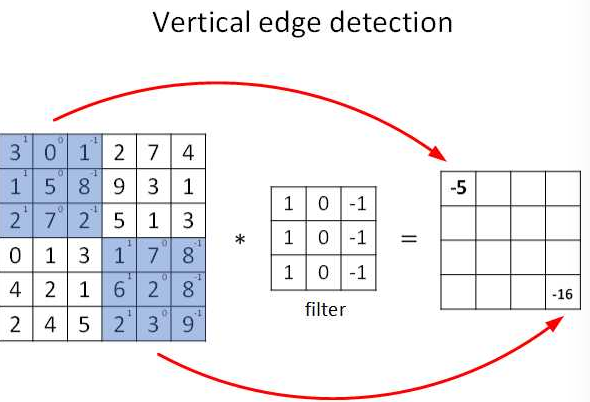 根据上图可知,卷积运算过程为从左到右,从上到下,每次在原始图中取与滤波器同等大小的一部分,每一部分中的值与滤波器中的值对应相乘(逐元素相乘)然后求和,将结果组成一个新的矩阵输出,为方便理解,下图是卷积运算实现动图:
根据上图可知,卷积运算过程为从左到右,从上到下,每次在原始图中取与滤波器同等大小的一部分,每一部分中的值与滤波器中的值对应相乘(逐元素相乘)然后求和,将结果组成一个新的矩阵输出,为方便理解,下图是卷积运算实现动图: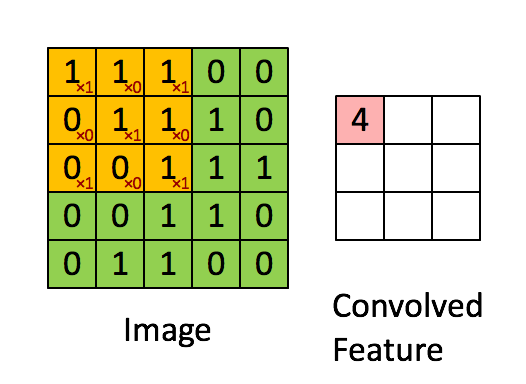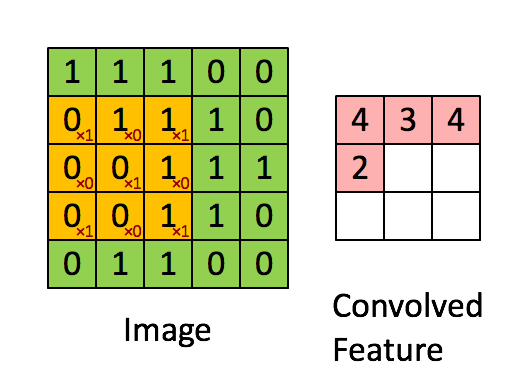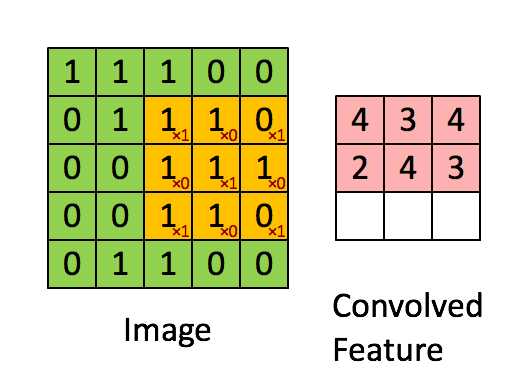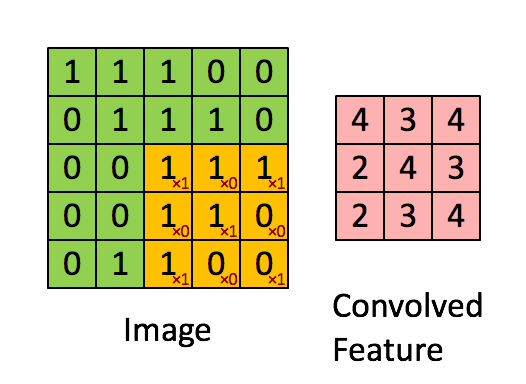 下图是垂直边缘检测的另一个例子,解释为什么下图中的滤波器可以做垂直边缘检测:
下图是垂直边缘检测的另一个例子,解释为什么下图中的滤波器可以做垂直边缘检测: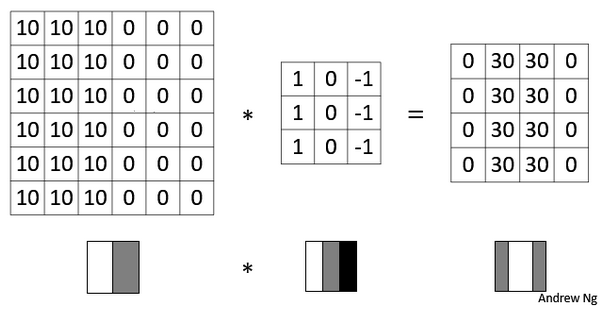 将上图中最右边的矩阵看作输出图片,则经过卷积后,输出图片中间白色区域对应输入图片中间的垂直边缘(区分白色和灰色的垂直线)。
将上图中最右边的矩阵看作输出图片,则经过卷积后,输出图片中间白色区域对应输入图片中间的垂直边缘(区分白色和灰色的垂直线)。
更多边缘检测例子
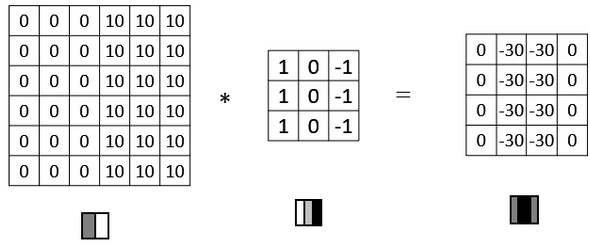 如果将灰度图左右数值进行翻转,再与之前的滤波器进行卷积,得到结果有区别。实际中,反映了由明变暗和由暗变明的两种渐变方式。如果不在乎两者的区别,可以对输出取绝对值。
如果将灰度图左右数值进行翻转,再与之前的滤波器进行卷积,得到结果有区别。实际中,反映了由明变暗和由暗变明的两种渐变方式。如果不在乎两者的区别,可以对输出取绝对值。
下图是垂直边缘检测和水平边缘检测滤波器: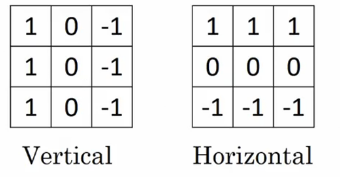 还有其他的滤波器,如
还有其他的滤波器,如 Sobel 滤波器和 Scharr 滤波器,其增加了中间一行的权重,提高了结果的稳健性。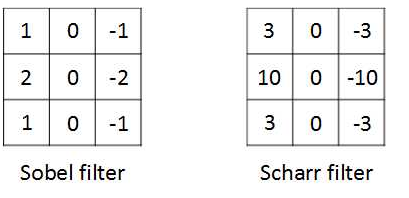 注意:实际中,不一定去使用那些研究者选择的滤波器数字,可以将滤波器中的数字看成参数,之后可以通过反向传播去学习这些参数。
注意:实际中,不一定去使用那些研究者选择的滤波器数字,可以将滤波器中的数字看成参数,之后可以通过反向传播去学习这些参数。
填充 ( Padding )
假如输入的图片大小是 \(n\times n \) 滤波器的大小是 \(f\times f \) ,则卷积后的输出大小是 \((n-f+1)\times (n-f+1)\) 。这样会存在两个缺点:
- 每次卷积运算后,输出的图形会缩小,例如从 \(6\times 6 \) 缩小到 \(4\times 4 \),经过几次后可能变为 \(1\times 1 \) 的大小。
- 那些在角落或者边缘区域的像素在输出中采用较少,意味着丢掉了图像边缘位置的许多信息。
为了解决这两个问题,需要在卷积操作之前对输入图像进行填充。就是在图像边缘再填充像素,通常填充 \(0\) 。如果用 p 表示每个方向填充的像素点的数量,下图的中 \(p=2 \) :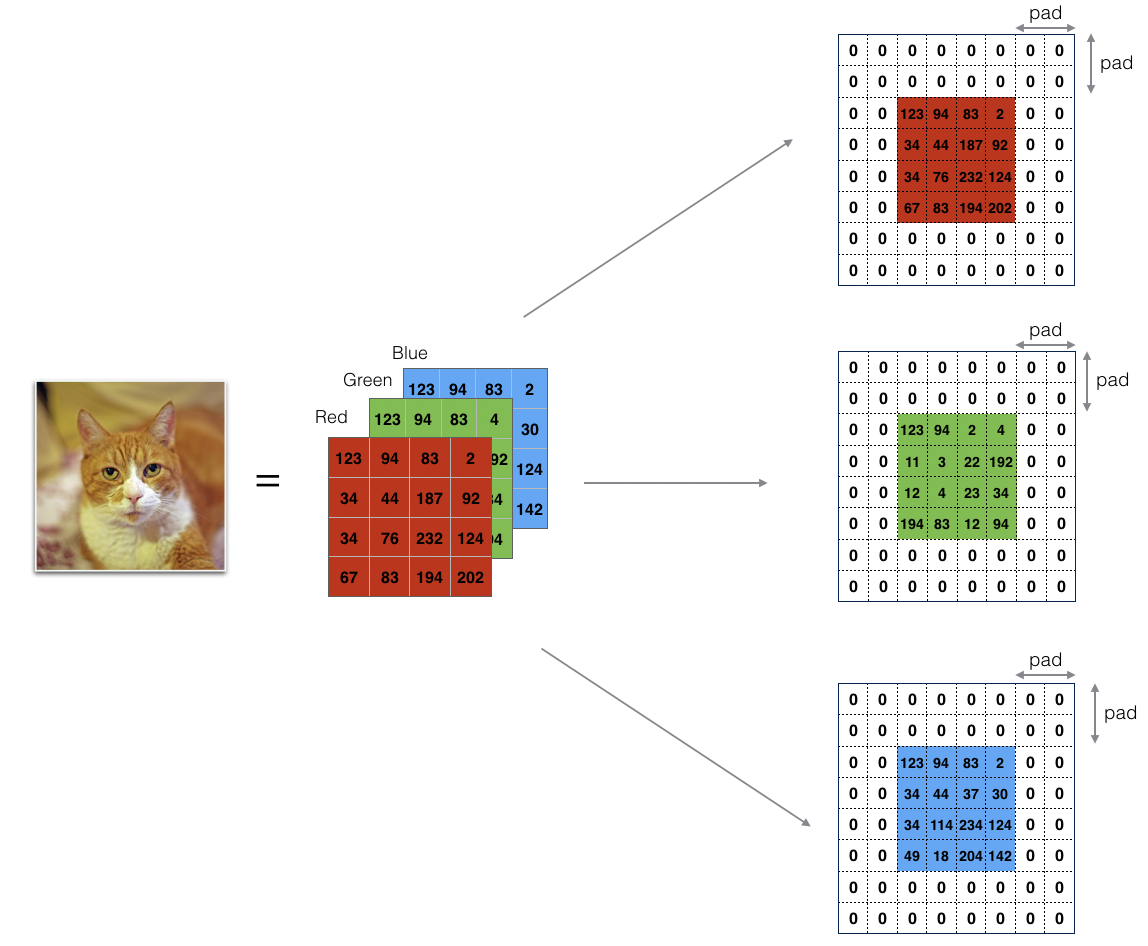 可知,填充后的图片大小是 \((n+2p)\times (n+2p)\) ,滤波器的大小是 \(f\times f \) ,则卷积后输出大小是 \((n+2p-f+1)\times (n+2p-f+1)\) 。
可知,填充后的图片大小是 \((n+2p)\times (n+2p)\) ,滤波器的大小是 \(f\times f \) ,则卷积后输出大小是 \((n+2p-f+1)\times (n+2p-f+1)\) 。
至于选择多少像素填充,有两种选择:
- Valid 填充:不填充( \(p=0 \) ),输出结果是 \((n-f+1)\times (n-f+1)\) 。
- Same 填充:填充使得输入和卷积后的输出的大小一样,需要 \(p=\dfrac {f-1}{2}\) 。
注意:一般情况下,\(f\) 通常是奇数。
卷积步长 ( Strided convolutions )
卷积步长是另一个构建卷积神经网络的基本操作。
步长表示滤波器在原始图像上水平或垂直方向上每次移动的距离。之前的步常默认为 \(1\) 。如果将步长设置为 \(2\) 则卷积过程如下图所示: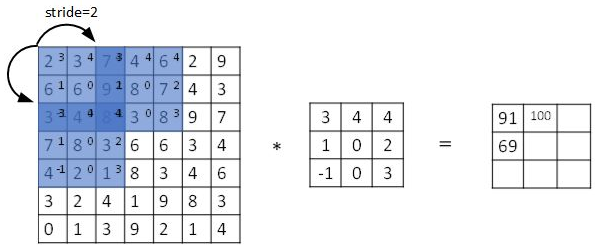 设步长为 s ,填充像素量为 p ,输入图片大小为 \(n\times n \) ,滤波器大小为 \(f\times f \) ,则卷积后的输出大小为:$$\lfloor {\dfrac {n+2p-f}{s}+1}\rfloor \times \lfloor {\dfrac {n+2p-f}{s}+1}\rfloor$$公式中的符号表示取整符号。
设步长为 s ,填充像素量为 p ,输入图片大小为 \(n\times n \) ,滤波器大小为 \(f\times f \) ,则卷积后的输出大小为:$$\lfloor {\dfrac {n+2p-f}{s}+1}\rfloor \times \lfloor {\dfrac {n+2p-f}{s}+1}\rfloor$$公式中的符号表示取整符号。
- 杂谈:
在机器学习中谈论的卷积实际上被称为互相关 (cross-correlation),不是数学意义上的卷积。数学上的卷积在做元素乘积求和之前,需要将滤波器沿水平和垂直轴翻转(相当于做镜像)。但按照机器学习惯例,通常不进行翻转操作。
高维卷积
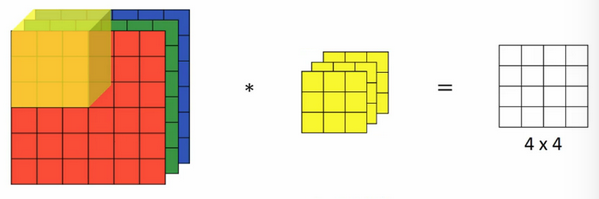 如果对三通道的
如果对三通道的 RGB 的图像 (\(6\times 6 \times 3 \)) 进行卷积操作,则对应的滤波器也同样是三通道的 (\(3\times 3\times 3 \))卷积的结果输出是 (\(4\times 4 \times 1\))。实现过程:将每个单通道与对应的滤波器(单通道)进行卷积,然后将三个通道相加,将 \(27\) 个值求和作为一个输出值。
不同的通道对应的滤波器可以不同。例如,如果只检测 R 通道的垂直边缘,则 G 和 B 通道对应的滤波器值可以全部设置为 \(0\) 。当输入有特定的高度、宽度和通道数时,滤波器可以有不同的高、宽,但必须有相同的通道数。
如果想同时检测垂直和水平边缘,或更多其他边缘(换句话说就是同时检测更多特征),可以增加滤波器个数。例如设置第一个滤波器检测垂直边缘,第二个滤波器检测水平边缘,最后将每个滤波器卷积的输出堆叠在一起,如下图所示: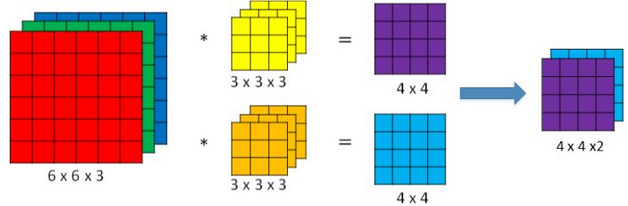 每个滤波器的输出对应一个特征。设输入的图像大小是 \(n\times n \times n_c\) (\(n_c \) 是通道数) ,滤波器大小是 \(f\times f \times n_c \) ,则卷积的输出是 \((n-f+1)\times (n-f+1)\times n’ _c \) ,其中 \(n’_c \) 为滤波器个数(默认步长为 \(1\))。
每个滤波器的输出对应一个特征。设输入的图像大小是 \(n\times n \times n_c\) (\(n_c \) 是通道数) ,滤波器大小是 \(f\times f \times n_c \) ,则卷积的输出是 \((n-f+1)\times (n-f+1)\times n’ _c \) ,其中 \(n’_c \) 为滤波器个数(默认步长为 \(1\))。
单层卷积网络 (one layer of a convolutional network)
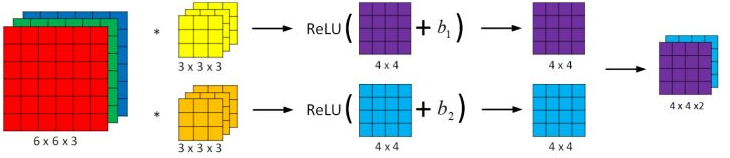 与之前的卷积过程相比较,卷积神经网络的单层结构多了激活函数和偏移量;而与标准神经网络:$$Z ^{[l]} = W ^{[l]}A ^{[l-1]}+ b$$$$A ^{[l]}= g ^{[l]}(Z ^{[l]})$$相比,滤波器的数值对应权重 \(W ^{[l]}\) ,卷积运算对应 \(W ^{[l]}\) 与 \(A ^{[l-1]}\) 的乘积运算,激活函数选择
与之前的卷积过程相比较,卷积神经网络的单层结构多了激活函数和偏移量;而与标准神经网络:$$Z ^{[l]} = W ^{[l]}A ^{[l-1]}+ b$$$$A ^{[l]}= g ^{[l]}(Z ^{[l]})$$相比,滤波器的数值对应权重 \(W ^{[l]}\) ,卷积运算对应 \(W ^{[l]}\) 与 \(A ^{[l-1]}\) 的乘积运算,激活函数选择 Relu 函数。
下面视频说明了单层卷积神经网络工作过程:
对于一个 \(3\times 3 \times 3 \) 的滤波器,包括偏移量 \(b\) 在内共有 \(28\) 个参数,不论输入的图像多大,参数始终是 \(28\) 。即选定滤波器组后,参数的数目与输入的图片尺寸无关,因此对比标志神经网络,卷积神经网络的参数要少的多,这是卷积神经网络 (
CNN) 的优点之一。符号总结
设 \(l\) 层为卷积层,则:
- \(f ^{[l]}\) :滤波器的高或宽;
- \(p ^{[l]}\) :填充的像素数量;
- \(s ^{[l]}\) :步长;
- \(n _c ^{[l]}\) :滤波器的个数;
- 输入维度:\(n _H ^{[l-1]}\times n _W ^{[l-1]}\times n _c ^{[l-1]}\) ,其中 \(n _H ^{[l-1]}\) 表示输入图像高度,\(n _W ^{[l-1]}\) 表示输入图像宽度。
- 输出维度:\(n _H ^{[l]}\times n _W ^{[l]}\times n _c ^{[l]}\) ,其中:$$n _H ^{[l]} = \lfloor {\dfrac {n _H ^{[l-1]}+2p ^{[l]}-f ^{[l]}}{s ^{[l]}}+1}\rfloor$$$$n _W ^{[l]} = \lfloor {\dfrac {n _W ^{[l-1]}+2p ^{[l]}-f ^{[l]}}{s ^{[l]}}+1}\rfloor$$
- 每个滤波器的维度是:\(f ^{[l]}\times f ^{[l]}\times n _c ^{[l-1]}\) ,其中 \(n _c ^{[l-1]}\) 为输入图像的通道数(也称为深度);
- 权重维度:\(f ^{[l]}\times f ^{[l]}\times n _c ^{[l-1]}\times n _c ^{[l]}\) ;
- 偏置维度:\(1\times 1 \times 1 \times n _c ^{[l]}\)。
注:不同的文献可能对高度、宽度、通道数的顺序表示不同。
简单卷积网络示例
一个简单的 CNN 神经网络如下图所示: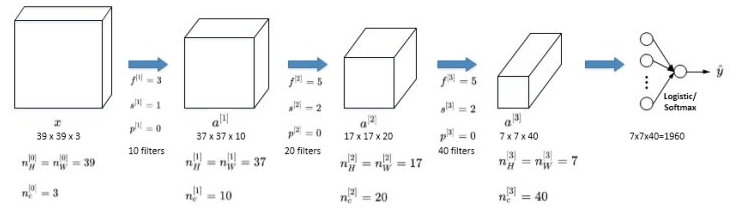 图中 \(a ^{[3]}\) 的维度为 \(7\times 7 \times 40 \) ,将 \(1960\) 个特征拉伸为一列,作为最后一层的输入。
图中 \(a ^{[3]}\) 的维度为 \(7\times 7 \times 40 \) ,将 \(1960\) 个特征拉伸为一列,作为最后一层的输入。
随着神经网络的深度的不断加深,输出的图像的高度 \(n _H ^{[l]}\) 和宽度 \(n _W ^{[l]}\) 不断减小,但 \(n _c ^{[l]}\)在不断增加。
一个典型的卷积神经网络通常有三种层:卷积层 (Convolution layer)、池化层 (Pooling layer) 、全连接层 (Fully Connected layer)。
池化层
池化层可用来缩减模型大小、提高计算速度、同时提高所提取特征的鲁棒性。
实际中,采用较多的一种池化过程叫最大化池化 (Max Pooling)。将输入拆分为不同的区域,输出的每个元素都是对应区域的最大值,如下图所示: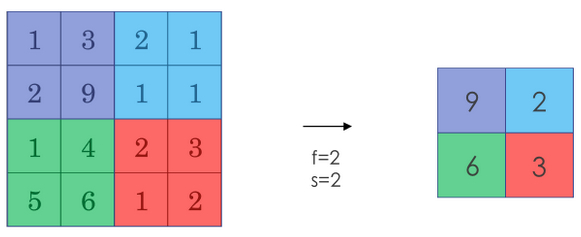 池化过程类似于卷积过程,上图中的池化过程相当于使用了大小 \(f=2\) 的滤波器,且步长为 \(s=2\) 。卷积过程的公式同样也适用于池化过程。如果输入有多个通道,则分别对每个通道执行池化过程,因此输入的通道数和输出的通道数一样。
池化过程类似于卷积过程,上图中的池化过程相当于使用了大小 \(f=2\) 的滤波器,且步长为 \(s=2\) 。卷积过程的公式同样也适用于池化过程。如果输入有多个通道,则分别对每个通道执行池化过程,因此输入的通道数和输出的通道数一样。
- 杂谈:最大池化过程的直观理解
元素值较大可能意味着池化过程之前的卷积过程提取到了某些特定的特征,池化过程中的最大化操作使得只要在一个区域内提取到某个特征,它都会保留在最大池化的输出中。
另一种池化过程是平均池化 (Average Pooling)。将从取某个区域最大值改为取这个区域的平均值作为输出(用的较少)。平均池化过程如下图所示: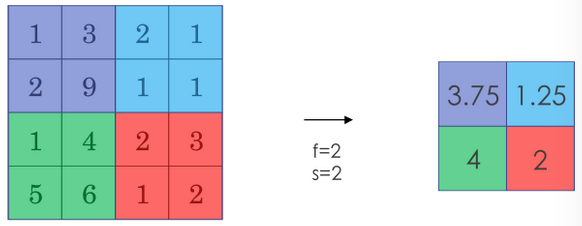 注意:池化过程有一组超参数(大小 \(f\) ,步长 \(s\) ,及选择最大池化还是平均池化)但没有参数需要学习。填充参数 \(p\) 很少用。
注意:池化过程有一组超参数(大小 \(f\) ,步长 \(s\) ,及选择最大池化还是平均池化)但没有参数需要学习。填充参数 \(p\) 很少用。
池化过程的输入维度为:$$n _H\times n _W\times n _c$$输出维度为:$$\lfloor {\dfrac {n _H -f}{s}+1}\rfloor \times \lfloor {\dfrac {n _W -f}{s}+1}\rfloor\times n _c$$
卷积神经网络示例
下图是一个识别数字的卷积神经网络的结构(类似 LeNet-5 网络): 建议:计算神经网络的层数时,通常只统计具有权重和参数的层,因此池化层和之前的卷积层记为一层。
建议:计算神经网络的层数时,通常只统计具有权重和参数的层,因此池化层和之前的卷积层记为一层。
图中的 FC3 和 FC4 为全连接层,与标准的神经网络一致。整个神经网络的参数如下图所示: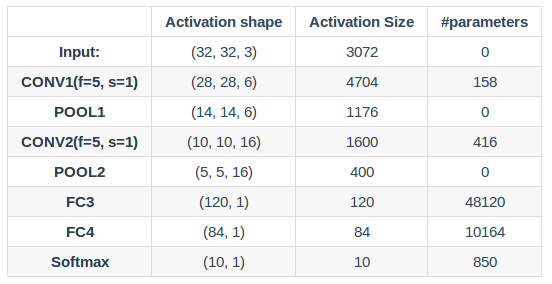
使用卷积神经网络原因
和标准神经网络对比,对于大量的输入数据,CNN 有效减小了参数的数量,原因如下:
- 参数共享 (Parameter sharing):特征检测如果适用于图片的某个区域,那么它也可能适用于图片的其他区域。即在卷积过程中,不管输入有多大,一个特征探测器(滤波器)就能对整个输入的某一特征进行探测。
- 稀疏连接 (Sparsity of connections):在每一层中,由于滤波器的尺寸限制,输入和输出之间的连接是稀疏的,每个输出值只取决于输入在局部的一小部分值。
池化过程则在卷积后很好地聚合了特征,通过降维来减少运算量。
由于 CNN 参数数量较小,所需的训练样本就相对较少,因此在一定程度上不容易发生过拟合现象。并且 CNN 比较擅长捕捉区域位置偏移(捕捉平移不变)。即进行物体检测时,不太受物体在图片中位置的影响,增加检测的准确性和系统的健壮性。
深度卷积网络:实例探究
本节涉及的神经网络实例包括:
- LeNet-5
- AlexNet
- VGG
此外还涉及 Resnet (Residual Network, 残差网络) 和 Inception Neural Network 。
经典网络
LeNet-5
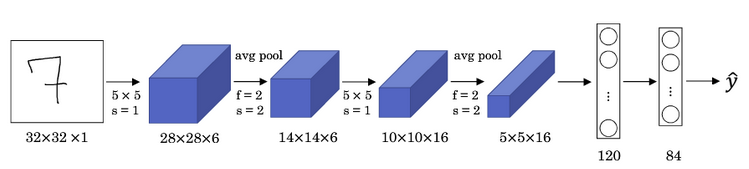 该网络具有的特点如下:
该网络具有的特点如下:
LeNet-5针对灰度图像训练,输入图像的通道数为 \(1\) ;- 该网络模型包含参数少(此例中大约 \(6\) 万个),远少于现代神经网络的参数;
- 针对分类问题,现代版本中输出层使用
Softmax函数(图中含有 \(84\) 个节点的层作为Softmax的输入; - 该网络包含一种模式至今常用到,就是一个或多个卷积层后跟着一个池化层,然后又是若干个卷积层再接一个池化层,然后是全连接层,最后是输出;
LeNet-5网络被提出时,其池化层使用平均池化,各层的激活函数一般选择Sigmoid和tanh。现在,根据需要可以做出改进,例如使用最大池化,激活函数选择Relu函数。
AlexNet
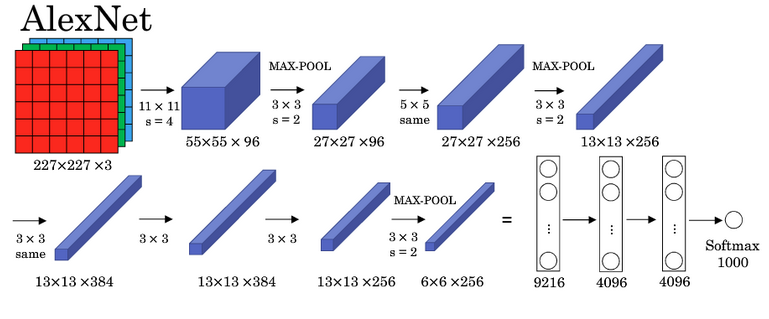 该网络具有的特点如下:
该网络具有的特点如下:
AlexNet模型与LeNet-5模型类似,但更加复杂(此例中包含大约 \(6000\) 万个参数。AlexNet模型使用了Relu激活函数;- 当用于训练图像和数据集时,
AlexNet网络结构能够处理非常相似的基本构造块,这些模块往往包含大量的隐藏单元或数据。
相关论文参考:Krizhevsky et al.,2012. ImageNet classification with deep convolutional neural networks
VGG
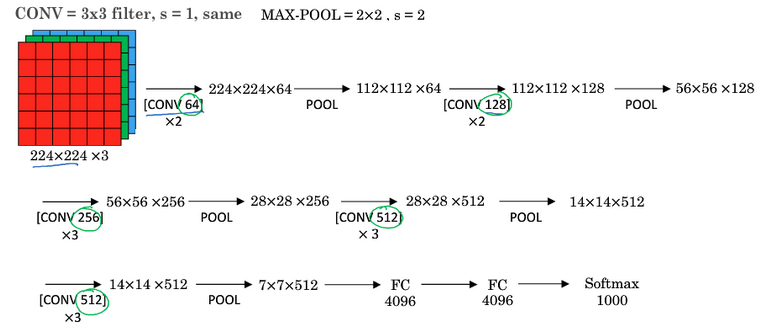 该网络具有的特点如下:
该网络具有的特点如下:
VGG又称为VGG-16,其中数字 \(16\) 表示网络中包含 \(16\) 个卷积层和全连接层;- 结构不复杂且规整(都是几个卷积层后面跟着可以压缩图像大小的池化层),卷积层的滤波器数量在每一步翻倍,或者说在每一组卷积层进行过滤器翻倍操作。
- 主要缺点是需要训练的特征数量非常大。
相关论文参考:Simonvan & Zisserman 2015. Very deep convolutional networks for large-scale image recognition
残差网络 (Residual Networks, ResNets)
The main benefit of a very deep network is that it can represent very complex functions. It can also learn features at many different levels of abstraction, from edges (at the lower layers) to very complex features (at the deeper layers). However, using a deeper network doesn’t always help. A huge barrier to training them is vanishing gradients: very deep networks often have a gradient signal that goes to zero quickly, thus making gradient descent unbearably slow. More specifically, during gradient descent, as you backprop from the final layer back to the first layer, you are multiplying by the weight matrix on each step, and thus the gradient can decrease exponentially quickly to zero (or, in rare cases, grow exponentially quickly and “explode” to take very large values).
由于存在梯度消失和梯度爆炸问题,很深的网络往往很难训练。残差网络 (ResNets)可有效解决这个问题。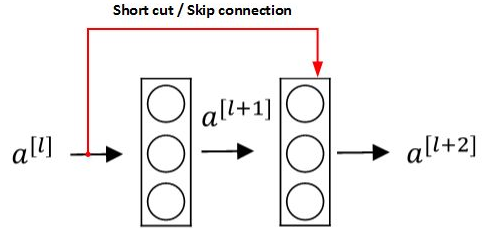 上图是残差块 (Residual block)。通过捷径 (
上图是残差块 (Residual block)。通过捷径 ( Short cut,或者称为 Skip connections 跳远连接)将 \(a ^{[l]}\) 添加到第二个 Relu 中,直接建立 \(a ^{[l]}\) 和 \(a ^{[l+2]}\) 的连接。对应的表达式如下:$$z ^{[l+1]}=W ^{[l+1]}a ^{[l]}+b ^{[l+1]}$$$$a ^{[l+1]}=g(z ^{[l+1]})$$$$z ^{[l+2]}=W ^{[l+2]}a ^{[l+1]}+b ^{[l+2]}$$$$a ^{[l+2]}=g(z ^{[l+2]}+a ^{[l]})$$构建一个残差网络就是将许多残差块堆叠在一起,形成一个很深的网络,如下图所示: 理论上,随着网络深度的加深,性能应该越来越好。但实际中,一个普通网络,随着神经网络层数增加,训练误差会先下降后上升。残差网络在训练集上会表现越来越好。如下图所示:
理论上,随着网络深度的加深,性能应该越来越好。但实际中,一个普通网络,随着神经网络层数增加,训练误差会先下降后上升。残差网络在训练集上会表现越来越好。如下图所示: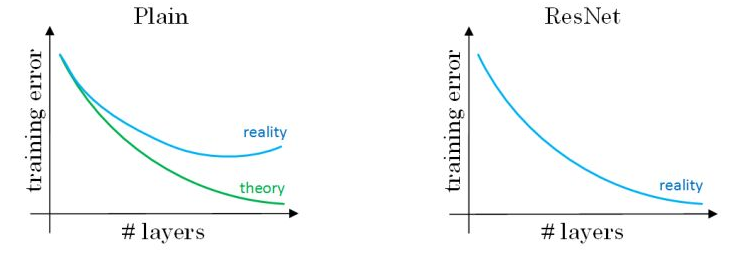 残差网络有助于解决梯度消失和梯度爆炸问题,让我们在训练更深网络的同时,又能保证良好的性能。
残差网络有助于解决梯度消失和梯度爆炸问题,让我们在训练更深网络的同时,又能保证良好的性能。
残差网络有效的原因
假设有一个大型神经网络,输入是 X ,输出是 \(a ^{[l]}\) 。给这个神经网络添加额外的两层,输出为 \(a ^{[l+2]}\) 。将这两层看层一个残差块,为便于说明,假设整个网络使用 Relu 激活函数。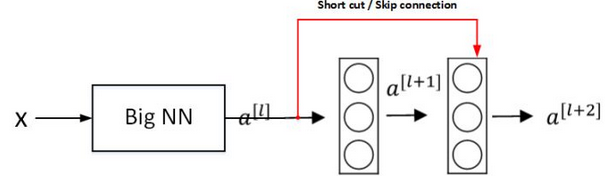 根据上图有:$$\begin {align} a ^{[l+2]} &=g(z ^{[l+2]}+a ^{[l]})\\&= g(W ^{[l+2]}a ^{[l+1]}+ b ^{[l+2]}+ a ^{[l]}) \end {align}$$当发生梯度消失时,有 \(W ^{[l+2]}\approx 0\) 方便说明令 \(b ^{[l+2]}\approx 0\) 则有:$$a ^{[l+2]}=g(a ^{[l]})=\text {Relu}(a ^{[l]})= a ^{[l]}$$说明增加的两层至少不会降低神经网络的性能(不论是把残差块添加到神经网络的中间还是末端位置)。如果增加的两层隐藏单元学习到了一些有用的信息,则可能会使网络的表现进一步提高。
根据上图有:$$\begin {align} a ^{[l+2]} &=g(z ^{[l+2]}+a ^{[l]})\\&= g(W ^{[l+2]}a ^{[l+1]}+ b ^{[l+2]}+ a ^{[l]}) \end {align}$$当发生梯度消失时,有 \(W ^{[l+2]}\approx 0\) 方便说明令 \(b ^{[l+2]}\approx 0\) 则有:$$a ^{[l+2]}=g(a ^{[l]})=\text {Relu}(a ^{[l]})= a ^{[l]}$$说明增加的两层至少不会降低神经网络的性能(不论是把残差块添加到神经网络的中间还是末端位置)。如果增加的两层隐藏单元学习到了一些有用的信息,则可能会使网络的表现进一步提高。
如果 \(a ^{[l]}\) 和 \(a ^{[l+2]}\) 的维度不同,需要引入矩阵 \(W _s \) 与 \(a ^{[l]}\) 相乘,使得二者的维度相同。矩阵 \(W _s \) 可以是模型学习得到,或者是一个固定矩阵,使得 \(a ^{[l]}\) 截断或补 \(0\) 。下图是论文中的残差网络的一个典型结构: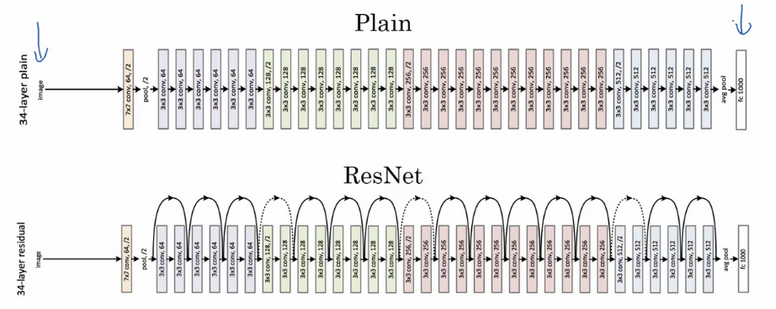 卷积层通常使用
卷积层通常使用 same 卷积以保持维度相同。
相关论文:He et al., 2015. Deep residual networks for image recognition
\(1\times 1\) 卷积
\(1\times 1\) 卷积(或者称为 Network in Network)指滤波器的大小为 \(1\) 。当输入通道为 \(1\) 时,\(1\times 1\)卷积意味着乘积操作(似乎没啥用)。如下图所示: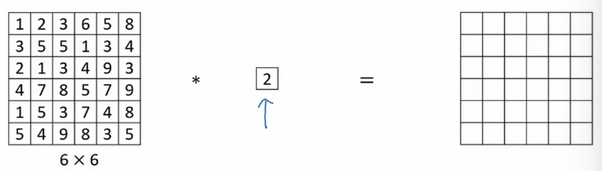 当输入通道数更多时,例如下图中的 \(32\) 个通道,\(1\times 1\) 卷积可以从根本上理解对这 \(32\) 个不同位置都应用一个全连接层。可用于降低或升高数据的维度(取决于滤波器的个数)。
当输入通道数更多时,例如下图中的 \(32\) 个通道,\(1\times 1\) 卷积可以从根本上理解对这 \(32\) 个不同位置都应用一个全连接层。可用于降低或升高数据的维度(取决于滤波器的个数)。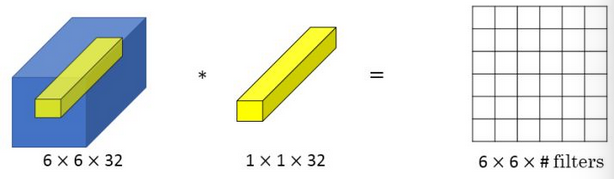 池化层可以压缩输入的高度 (\(n _H\)) 和宽度 (\(n _W\)),而 \(1\times 1\) 卷积可以压缩输入的通道数 (\(n _c\)),取决于用多少个滤波器。例如下图中用 \(32\) 个大小为 \(1\times 1\times 192\) 的滤波器进行卷积,将输入数据通道数从 \(192\) 压缩为 \(32\) 。
池化层可以压缩输入的高度 (\(n _H\)) 和宽度 (\(n _W\)),而 \(1\times 1\) 卷积可以压缩输入的通道数 (\(n _c\)),取决于用多少个滤波器。例如下图中用 \(32\) 个大小为 \(1\times 1\times 192\) 的滤波器进行卷积,将输入数据通道数从 \(192\) 压缩为 \(32\) 。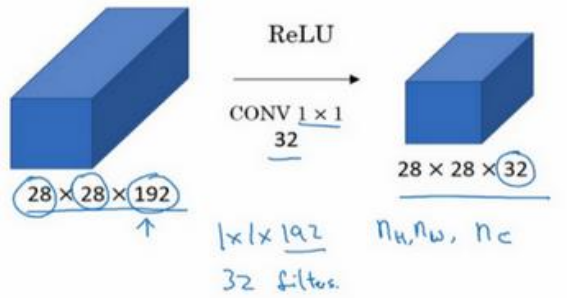
Inception 网络
Inception网络不需要人为决定使用哪种滤波器 (\(1\times 1\) 还是 \(3\times 3\)等) 或者是否需要池化,而是由网络自行确定这些参数,可以给网络添加这些参数的所有可能值,然后将这些对应的输出连接起来,让网络自己学习它需要什么样的参数,采用哪些滤波器组合。
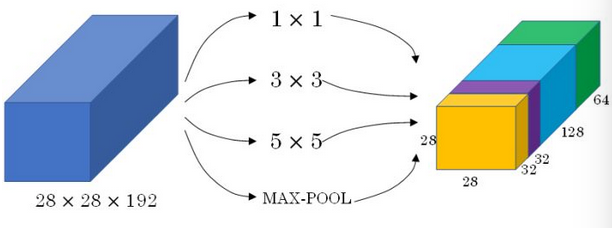 为了使得输出组合时维度匹配,
为了使得输出组合时维度匹配,Inception 网络选择不同大小的滤波器进行 same 卷积。
在提升性能的同时, Inception 网络有较大的计算成本问题,下面以 \(5\times 5\) 大小的卷积为例说明: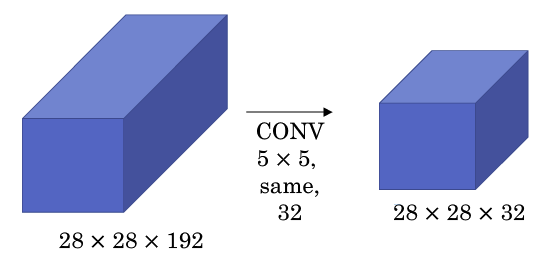 图中有 \(32\) 个滤波器,每个滤波器大小为 \(5\times 5 \times 192\) ,输出大小为 \(28\times 28\times 32\) ,因此需要计算 \(28\times 28\times 32\) 个数字,对于每个数字,需要执行 \(5\times 5\times 192\) 次乘法,加法和乘法运算次数近似相等。因此,此层的计算量为 \(28\times 28\times 32\times 5\times 5\times 192 =1.2\) 亿。
图中有 \(32\) 个滤波器,每个滤波器大小为 \(5\times 5 \times 192\) ,输出大小为 \(28\times 28\times 32\) ,因此需要计算 \(28\times 28\times 32\) 个数字,对于每个数字,需要执行 \(5\times 5\times 192\) 次乘法,加法和乘法运算次数近似相等。因此,此层的计算量为 \(28\times 28\times 32\times 5\times 5\times 192 =1.2\) 亿。
为了解决计算量大的问题,引入 \(1\times 1\) 卷积(有时候称为瓶颈层),如下图: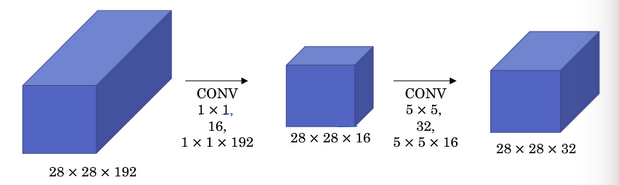 同理可以计算出引入 \(1\times 1\) 卷积后,计算量变为 \(1024\) 万,大大降低了计算量。
同理可以计算出引入 \(1\times 1\) 卷积后,计算量变为 \(1024\) 万,大大降低了计算量。
注:只要合理构建瓶颈层,既可以显著缩小表示层规模,又不会降低网络性能,从而节省计算。
完整的 Inception 网络
下图是引入 \(1\times 1\) 卷积后的 Inception 模块: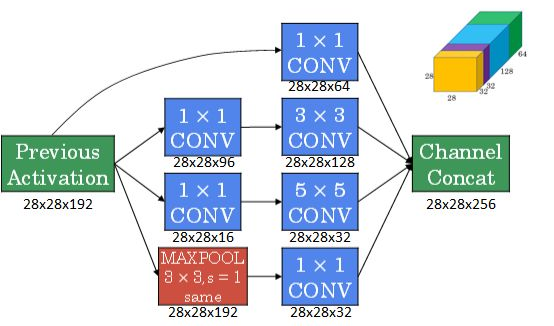 使用
使用 same 类型的 padding 来池化,使得输出的高度和宽度和输入保持一致。由于池化层不改变输入的通道数,因此需要加一个 \(1\times 1\) 卷积层将输入通道压缩。
多个 Inception 模块组成一个完整的 Inception 网络,如下图所示: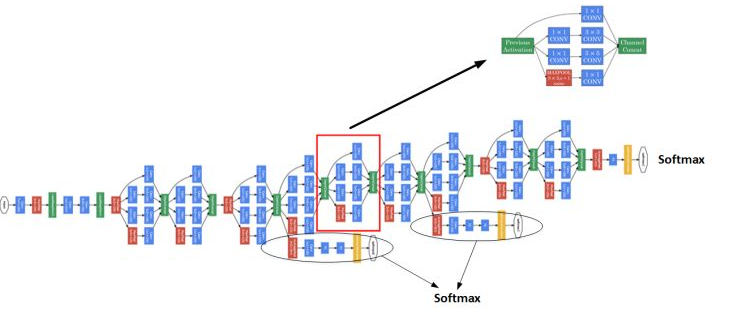 图中圈起来的隐藏层用于
图中圈起来的隐藏层用于 softmax 输出,他们确保了即便是隐藏单元和中间层也参与特征计算,在 Inception 网络中起到一种调整效果,并且可以防止网络发生过拟合。
相关论文:Szegedy et al., 2014, Going Deeper with Convolutions
使用开源的实现方案
很多神经网络复杂细致,并充斥着参数调节的细节问题,因而很难仅通过阅读论文来重现他人的成果。想要搭建一个同样的神经网络,查看开源的实现方案会快很多。
某些网络通常都需要很长的时间来训练,而或许有人已经使用多个 GPU,通过庞大的数据集预先训练了这些网络,这样一来你就可以使用这些网络进行迁移学习。
迁移学习
迁移学习在之前已有介绍。相比于从头训练权重,下载别人已经训练好的网络结构的权重,用其做预训练,然后转换到自己感兴趣的任务上,有助于加速开发。
对于已训练好的卷积神经网络,可以将所有层都看作是冻结的,只需要训练与你的 Softmax 层有关的参数即可。如下图所示: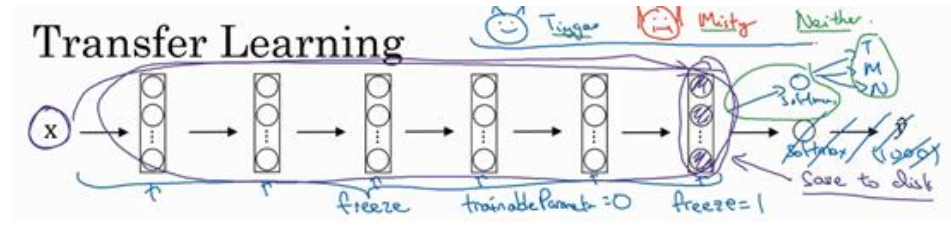 冻结的层由于不需要改变和训练,可以看作一个固定函数。可以将这个固定函数存入硬盘,以便后续使用,而不必每次再使用训练集进行训练了。
冻结的层由于不需要改变和训练,可以看作一个固定函数。可以将这个固定函数存入硬盘,以便后续使用,而不必每次再使用训练集进行训练了。
上述的做法适用于你只有一个较小的数据集。如果你有一个更大的数据集,应该冻结更少的层,然后训练后面的层。越多的数据意味着冻结越少的层,训练更多的层。如果有一个极大的数据集,你可以将开源的网络和它的权重整个当作初始化(代替随机初始化),然后训练整个网络。
数据扩增
当数据量小时,数据扩增 ( Data Augmentation) 可能会有帮助。常用的数据扩增包括镜像翻转、随机裁剪、色彩转换。其中,色彩转换是对图片的 RGB 通道数值进行随意增加或者减少,改变图片色调。关于 PCA 颜色增强可以查阅相关文献或代码。
在构建大型神经网络的时候,数据扩增和模型训练可以由两个或多个不同的线程并行来实现。
总结
在模型研究或者竞赛方面,有一些方法能够有助于提升神经网络模型的性能:
- 集成(
Ensembling):独立地训练几个神经网络,并平均输出它们的输出; Multi-crop at test time:将数据扩增应用到测试集,对结果进行平均。
由于这些方法计算和内存成本较大,一般不适用于构建实际的生产项目。
目标检测
目标定位
定位分类问题不仅需要识别判断出图片中物体的种类,还需要在图片中标记出其具体位置,用边框 ( Bounding Box )将物体圈起来。定位分类问题通常只有一个较大的对象位于图片中间位置,需要对它进行识别和定位。在对象检测中,图片可能含有多个对象,甚至单张图片中会有多个不同的对象。
为了定位图片中的汽车位置,可以让神经网络多输出 \(4\) 个数字,标记为 \(b _x \) 、\(b _y \) 、\(b _h \) 、\(b _w \) 。将图片左上角标记为 \((0,0)\) 右下角标记为 \((1,1)\) 如下图所示: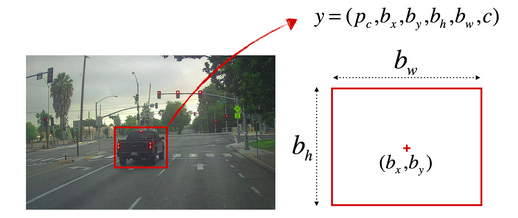
If you have 80 classes that you want YOLO to recognize, you can represent the class label c either as an integer from 1 to 80, or as an 80-dimensional vector (with 80 numbers) one component of which is 1 and the rest of which are 0. The video lectures had used the latter representation.
图中 \(P _c \) 表示是否含有物体,若含有物体则 \(P _c =1\) 若不含物体则 \(P _c =0\) 。对应的 \(y\) 标签如下:$$\begin {align}P _c =1, y=\begin {bmatrix}1 \\ b _x \\ b _y \\ b _h \\ b _w \\ c \end {bmatrix}& &P _c =0, y=\begin {bmatrix}0 \\ ? \\ ? \\ ? \\ ? \\ ? \end {bmatrix}\end {align}$$损失函数表示为 \(L(\widehat y , y)\) 若采用平方误差损失,则计算损失函数如下:
- 当 \(P _c =1 \) 即 \(y _1 =1\):\(L(\widehat y , y)=(\widehat {y} _1 - y _1) ^2 + \ldots + (\widehat {y} _n - y _n) ^2\) ;
- 当 \(P _c =0 \) 即 \(y _1 =0\):\(L(\widehat {y} , y)=(\widehat {y} _1 - y _1) ^2\)。
对于损失函数,通常做法是对边界框坐标应用平方差或类似方法,对 \(P _c =1\) 应用逻辑回归函数,甚至采用平方预测误差也是可以的。
特征点检测
神经网络可以输出图片上的特征点来实现对目标特征的识别(类似于标识对象的中心点位置那样)。在标签中(预测标签和实际标签),特征点以多个二维坐标的形式表示。
检测人脸的特征点可以进行情绪分类与判断,或者应用 AR 等领域。也可以通过特征点检测人体的姿态。
目标检测
目标检测采用基于滑动窗口的目标检测 (Sliding Windows Detection)(因为一张图中可能有多个对象,一张图中有一个对象训练较容易,对于有多个对象,所以滑动窗口是比较好的方法)。该算法的步骤如下(以汽车检测算法为例):
- 创建一个标签数据集,即适当剪切汽车图片样本,使得汽车位于中间位置(整张图片几乎被汽车占据);

- 利用构建的标签数据集训练
CNN网络; - 选择大小合适窗口和适当的步幅,对测试图片从左到右,从上到下滑动遍历。每个窗口都输入到训练好的
CNN神经网络进行预测。
滑动窗口目标检测的缺点是计算成本高,因为每次滑动都要进行一次 CNN 网络计算。增大步幅可以减小计算,但可能会影响性能。
卷积的滑动窗口实现
相较于普通的滑动窗口目标检测(从较大的图片多次截取,分别输入网络计算),基于卷积的滑动窗口目标检测可以提高运行速度。为了实现基于卷积的滑动窗口目标检测,首先需要将全连接 (FC)层转化为卷积层,如下图所示: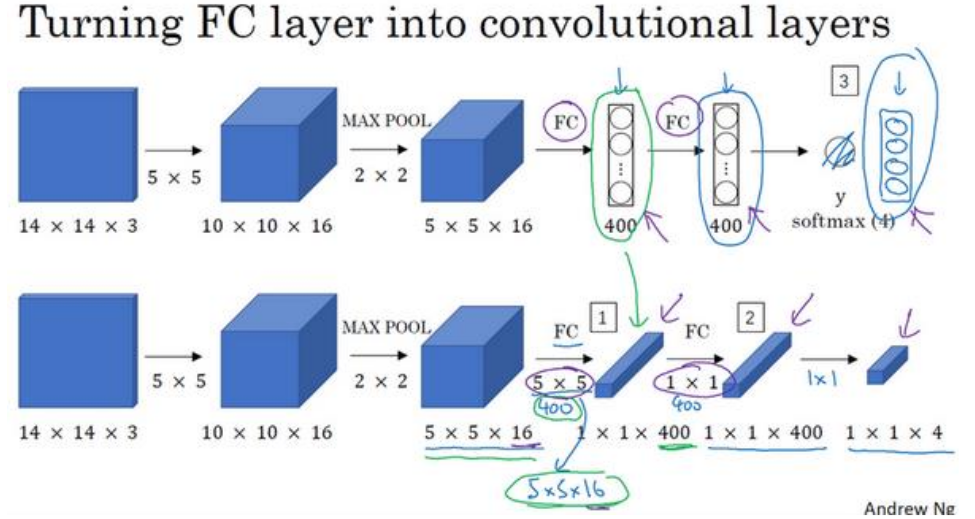 对于全连接层,用 \(5\times 5\times 16\) 的滤波器,数量为 \(400\) 个来实现,输出维度为 \(1\times 1\times 400\) 。从数学上看,经过卷积的输出和全连接层一样,因为这 \(400\) 个节点中每一个都有一个 \(5\times 5\times 16\) 的滤波器,其每个值都是上一层这些 \(5\times 5\times 16\) 激活值经过某个线性函数的输出结果。对于下一个全连接层,用 \(1\times 1\times 400\) 的滤波器,数量为 \(400\) 来实现,输出维度为 \(1\times 1\times 400\)。
对于全连接层,用 \(5\times 5\times 16\) 的滤波器,数量为 \(400\) 个来实现,输出维度为 \(1\times 1\times 400\) 。从数学上看,经过卷积的输出和全连接层一样,因为这 \(400\) 个节点中每一个都有一个 \(5\times 5\times 16\) 的滤波器,其每个值都是上一层这些 \(5\times 5\times 16\) 激活值经过某个线性函数的输出结果。对于下一个全连接层,用 \(1\times 1\times 400\) 的滤波器,数量为 \(400\) 来实现,输出维度为 \(1\times 1\times 400\)。
卷积滑动窗口的示例如下图所示: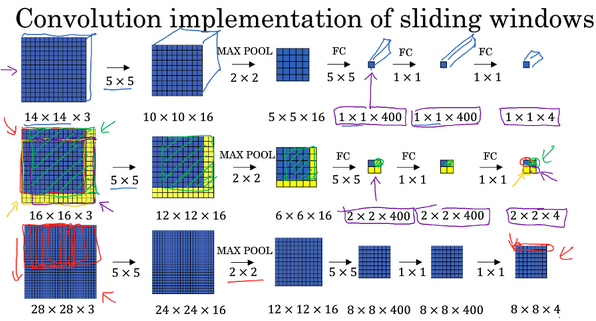 如图,对于 \(16\times 16\times 3\) 的图片,将其整张输入给网络进行计算(不是把输入图形分割为四个子集,分别执行前向传播)。输出维度是 \(2\times 2\times 4\) (步长为 \(2\) ),其中 \(2\times 2\) 表示有 \(4\) 个窗口结果。对于更大的 \(28\times 28\times 3\) 图片,输出是 \(8\times 8\times 4\) ,对应有 \(64\) 个窗口结果。
如图,对于 \(16\times 16\times 3\) 的图片,将其整张输入给网络进行计算(不是把输入图形分割为四个子集,分别执行前向传播)。输出维度是 \(2\times 2\times 4\) (步长为 \(2\) ),其中 \(2\times 2\) 表示有 \(4\) 个窗口结果。对于更大的 \(28\times 28\times 3\) 图片,输出是 \(8\times 8\times 4\) ,对应有 \(64\) 个窗口结果。
卷积滑动窗口效率高的原因:各个窗口公共区域的计算可以共享,降低运算成本。但存在一个缺点就是边界框的位置可能不够准确。
相关论文:Sermanet et al., 2014. OverFeat: Integrated Recognition, Localization and Detection using Convolutional Networks
边框预测
YOLO (“you only look once”) is a popular algoritm because it achieves high accuracy while also being able to run in real-time. This algorithm “only looks once” at the image in the sense that it requires only one forward propagation pass through the network to make predictions. After non-max suppression, it then outputs recognized objects together with the bounding boxes.
YOLO (You only look once)算法能得到更精确的边框。该算法的结构如下: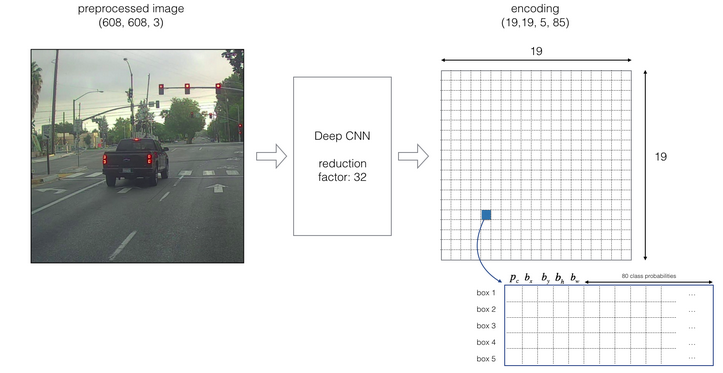
YOLO 算法将原始图片划分为 \(n\times n\) 网格(上图 \(n=19\) ),并将图像分类和定位算法逐一应用在每个网格,每个网格都有标签:$$\begin {bmatrix}P _c\\b _x\\b _y\\b _n\\b _w\\c \end {bmatrix}$$若某个目标的中心点落在某个网格,则该网格负责检测该对象。
这个算法的优点在于神经网络可以输出精确的边界框,测试的时候,输入图像 x ,跑正向传播,得到输出 y 可以得到 \(n\times n\) 个网格哪个有对象,且对应网格的标号以及相应的边界框信息,只要每个网格中对象没超过 \(1\) 个,这个算法就没问题。
算法具有如下优点:
- 与图像分类和目标定位算法类似,显示输出边框坐标和大小,不会受到滑动窗步幅大小的限制;
- 进行一次
CNN正向计算(单次卷积运算),效率很高,可以达到实时识别。
对于编码边框参数 \(b _x\),\(b _y\),\(b _h\),\(b _w\),YOLO 算法设 \(b _x\),\(b _y\),\(b _h\),\(b _w\) 的值是相对于网格比例。则有 \(b _x\),\(b _y\) 介于 \(0\) 和 \(1\)之间,\(b _h\),\(b _w\) 值可以大于 \(1\) 。这里只是给出一个通用的表示方法。
交并比
交并比 (Intersection over union) 是衡量定位精确度的一种方式。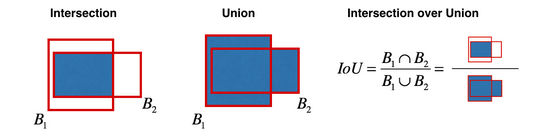
IoU 的值介于 \(0\) 和 \(1\) 之间,且约接近 \(1\) 说明目标定位越准确。当 \(\text {IoU}\geq 0.5\) 时,一般认为预测边框是正确的,当然也可以设置一个更高的域值。
非极大值抑制 (Non-max suppression)
非最大值意味着只输出概率最大的分类结果,但抑制很接近,但不是最大的其他预测结果。
YOLO 算法理论上只有一个网格检测一个对象,但实际上,可能有多个网格检测同一个对象。非极大值抑制可以确保算法对每个对象只检测一次。
非极大值抑制的步骤如下:
- 将包含目标中心的可行度 \(P _c\) 小于域值(例如 \(0.6\) )的网格丢弃;
- 选择拥有最大 \(P _c\) 的网格;
- 分别计算该网格和其他网格的
LoU,将LoU值超过阈值的网格丢弃; - 重复 \(2-3\) 步,直到不存在未处理的网格。
上述步骤适合于单类别目标检测,进行多个目标检测时,对于每个输出类别都分别做一次非极大值抑制。
Anchor Boxes
到目前为止,对象检测存在的一个问题是每个格子只检测一个对象,让一个格子检测多个对象,可以考虑 Anchor Boxes 。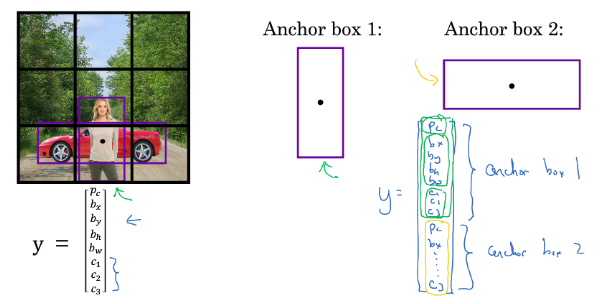 在上图示例中,我们希望同时检测人和汽车。因此,每个网格的的标签中含有两个
在上图示例中,我们希望同时检测人和汽车。因此,每个网格的的标签中含有两个 Anchor Box(当然可以设置更多的 Anchor Box ) 。输出的标签结果大小从 \(3\times 3\times 8\) 变为 \(3\times 3\times 16\)。若两个 \(P _c\) 都大于预设阈值,则说明检测到了两个目标。
在单目标检测中,图像中的目标被分配给了包含该目标中点的那个网格;引入 Anchor Box 进行多目标检测时,图像中的目标则被分配到了包含该目标中点的那个网格以及具有最高 IoU 值的该网格的 Anchor Box。Anchor Boxes 也有局限性,对于同一网格有三个及以上目标(但你有两个 Anchor Box ),或者两个目标的 Anchor Box 高度重合的情况处理不好。Anchor Box 的形状一般通过人工选取。高级一点的方法是用 k-means 将两类对象形状聚类,选择最具代表性的 Anchor Box。
YOLO 算法
将上述介绍的组合在一起,具体参考视频讲解。
相关论文:
You Only Look Once: Unified, Real-Time Object Detection
YOLO9000: Better, Faster, Stronger
候选区域 (Region proposals)
前面介绍的滑动窗口目标检测算法对一些明显没有目标的区域也进行了扫描,这降低了算法的运行效率。为了解决这个问题,R-CNN(Region CNN,带区域的 CNN) 被提出。通过对输入图片运行图像分割算法,在不同的色块上找出候选区域( Region Proposal ),就只需要在这些区域上运行分类器。
R-CNN 的缺点是运行速度慢,所以有一系列后续研究工作改进。例如 Fast R-CNN(与基于卷积的滑动窗口实现相似,但得到候选区域的聚类步骤依然很慢)、Faster R-CNN(使用卷积对图片进行分割)。不过大多数时候还是比 YOLO 算法慢。
相关论文:
- R-CNN: Girshik et al., 2013. Rich feature hierarchies for accurate object detection and semantic segmentation
- Fast R-CNN: Girshik, 2015. Fast R-CNN
- Faster R-CNN: Ren et al., 2016. Faster R-CNN: Towards real-time object detection with region proposal networks
特殊应用:人脸识别和神经风格转换
人脸识别
人脸识别 ( Face recognition ) 和人脸验证 ( Face verification ) 的区别:
- 人脸验证:
- Input image, name/ID
- Output whether the input image is that of the claimed person
- 人脸识别:
- Has a database of K persons
- Get an input image
- Output ID if the image is any of the K persons (or “not recognized” )
人脸识别问题要比人脸验证问题困难的多。
One-shot 学习
人脸识别面临的一个挑战是需要解决一次学习问题,意味着在大多数人脸识别应用中,需要通过单单一张图片或者一个人脸样例能去识别这个人。在一次学习问题中,只能通过一个样本进行学习,也能认出同一个人。一次学习是迁移学习的一种。
一个好的解决方法是学习 Similarity 函数,也就是说让神经网络学习一个用 d 表示的函数:$$d(\text {img1,img2}) = \text {degree of difference between images}$$以两张图片作为输入,输出两张图片的差异值。如果是同一个人,输出的差异值很小;如果是不同的人,输出的差异值很大。实际应用中可以设置一个阈值 \(\alpha\) 如果小于这个阈值则判断是同一个人,反之是不同的人。
Siamese 网络
学习 Similarity 函数的一种方式是使用 Siamese 网络,如下图所示: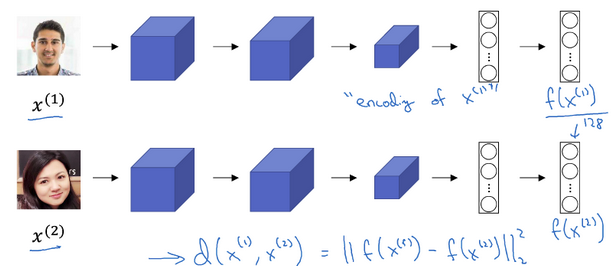 将图片 \(x ^{(1)}\),\(x ^{(2)}\) 分别输入两个相同的卷积网络中(实际上是一个网络,两个网络的参数完全一样),经过全连接层后得到特征向量 \(f(x ^{(1)})\),\(f(x ^{(2)})\) 。进而将 \(x ^{(1)}\),\(x ^{(2)}\) 的距离定义为这两幅图片的编码之差的范数:$$d(x ^{(1)},x ^{(2)})=||f(x ^{(1)})-f(x ^{(2)})|| _2 ^ 2$$需要做的就是学习参数(通过反向传播),使得如果两个输入是同一个人,得到的两个编码的距离就小。如何定义实际的目标函数(代价函数),可以利用三元损失函数达到这个目的。
将图片 \(x ^{(1)}\),\(x ^{(2)}\) 分别输入两个相同的卷积网络中(实际上是一个网络,两个网络的参数完全一样),经过全连接层后得到特征向量 \(f(x ^{(1)})\),\(f(x ^{(2)})\) 。进而将 \(x ^{(1)}\),\(x ^{(2)}\) 的距离定义为这两幅图片的编码之差的范数:$$d(x ^{(1)},x ^{(2)})=||f(x ^{(1)})-f(x ^{(2)})|| _2 ^ 2$$需要做的就是学习参数(通过反向传播),使得如果两个输入是同一个人,得到的两个编码的距离就小。如何定义实际的目标函数(代价函数),可以利用三元损失函数达到这个目的。
相关论文:Taigman et al., 2014, DeepFace closing the gap to human level performance
Triplet 损失
要想通过神经网络的参数来得到优质的人脸图片编码,方法之一是定义三元组损失函数,然后应用梯度下降法。Triplet 一词来源于训练这个神经网络需要大量的包含 Anchor (靶目标)、Positive (正例)、Negative (反例)的图片组,其中 Anchor (靶目标)和 Positive (正例)是同一个人的人脸图像,如下图所示: 对于一个三元组,应该满足:$$||f(A)-f(P)|| _2 ^2 +\alpha \leq ||f(A)-f(N)|| _2 ^2$$其中 \(\alpha \) 被称为间隔(
对于一个三元组,应该满足:$$||f(A)-f(P)|| _2 ^2 +\alpha \leq ||f(A)-f(N)|| _2 ^2$$其中 \(\alpha \) 被称为间隔( margin ) ,用于确保 \(f()\) 不会总输出 \(0\) (或者一个恒定的值)。Triplet 损失函数定义如下:$$L(A,P,N)=\text {max}(||f(A)-f(P)|| _2 ^2 -||f(A)-f(N)|| _2 ^2 +\alpha , 0)$$对于大小为 \(m\) 的训练集,代价函数为:$$J=\sum _{i=1} ^{m}L(A ^{(i)},P ^{(i)},N ^{(i)})$$通过梯度下降法来最小化代价函数。
选择三元组时,最好的做法是人为增加 Anchor 和 Positive 的区别,缩小 Anchor 和 Negative 的区别,促使模型去学习不同人脸之间的关键差异,而不是随机选择构建三元组。
为了构建三元组的数据集,需要同一个人的多张照片。如果只有一个人的一张照片,则根本无法训练这个系统。当然,训练完这个系统后,可以应用到一次学习问题上。
相关论文:Schroff et al., 2015, FaceNet: A unified embedding for face recognition and clustering
面部验证和二分类
Triplet 损失是一个学习人脸识别卷积网络参数的好方法。还有其他的方法,例如将人脸识别当成一个二分类问题。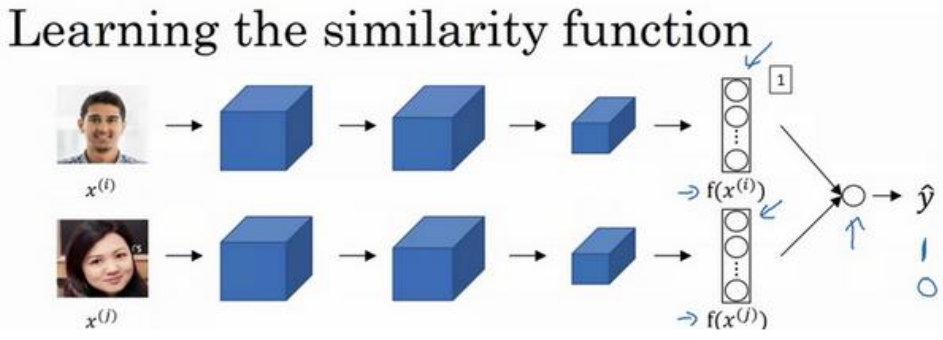 输入一对图片,将
输入一对图片,将 Siamese 网络产生的特征向量输入同一个 sigmoid 单元,输出 \(1\) 则表示识别为同一个人,输出 \(0\) 表示识别为不同的人。sigmoid 单元对应的表达式如下:$$\widehat y = \sigma \Big(\sum _{k=1} ^{K}w _i|f(x ^{(i)}) _k - f(x ^{(j)}) _k| +b\Big )$$上式中 \(w _k \) 和 \(b\) 是通过梯度下降法训练得到的参数,下标 \(k\) 表示特征向量中第 \(k\) 个特征值。
还有另外一种表示:$$\widehat y = \sigma \Big(\sum _{k=1} ^{K}w _i\dfrac {((f(x ^{(i)}) _k - f(x ^{(j)}) _k) ^2}{f(x ^{(i)}) _k + f(x ^{(j)}) _k} +b\Big )$$其中 \(\dfrac {(f(x ^{(i)}) _k - f(x ^{(j)}) _k) ^2}{f(x ^{(i)}) _k + f(x ^{(j)}) _k}\)被称为 \(\chi\) 相似度。
无论是对于使用 Triplet 损失函数的网络,还是二分类结构,为了减少计算量,可以提前计算好编码输出 f(x) 并保存。这样就不必存储原始图片,并且每次进行人脸识别时只需要计算测试图片的编码输出。
神经风格迁移
神经风格迁移是将参考风格图像的风格 “迁移” 到令一张图像中,生成具有其特色的图像。
深度卷积网络在学什么
 上图显示浅层的隐藏层通常检测出是原始图像的边缘,颜色,阴影等简单信息。随着层数的增加,隐藏单元能捕捉区域更大区域,学习的特征也更加复杂和具体。
上图显示浅层的隐藏层通常检测出是原始图像的边缘,颜色,阴影等简单信息。随着层数的增加,隐藏单元能捕捉区域更大区域,学习的特征也更加复杂和具体。
相关论文:Zeiler and Fergus., 2013, Visualizing and understanding convolutional networks
代价函数
要构建一个神经风格迁移系统,需要为生成的图像定义一个代价函数。代价函数如下:$$J(G)=\alpha J _{\text {content}}(C, G)+\beta J _{\text {style}}(S, G)$$其中 \(J _{\text {content}}(C, G)\) 度量生成图片 \(G\) 和内容图片 \(C\) 的相似性,\(J _{\text {style}}(S, G)\) 度量生成图片 \(G\) 和风格图像 \(S\) 的相似性。利用超参数 \(\alpha\) 和 \(\beta\) 权衡两种代价度量。
神经风格迁移的算法步骤如下:
- 随机生成图片 \(G\) 的所有像素点;
- 利用梯度下降法使得代价函数 \(J(G)\) 最小,不断修正 \(G\) 的像素点(\(G := G-\dfrac {\partial J(G)}{\partial G}\))。(注意:这个步骤中更新的是图像 \(G\) 的像素)
相关论文:Gatys al., 2015. A neural algorithm of artistic style
内容代价函数
内容代价函数 \(J _{\text {content}}(C, G)\) 计算过程如下:
- 使用一个预训练好的
CNN(例如VGG); - 选择某一个隐藏层
l来计算内容代价。l太小使得生成图片像素非常接近你的内容图片,l太大会使得内容图片里有狗,确保生成图片也有狗。实际中l通常选择中间层。 - 设 \(a ^{(C)[l]}\)、\(a ^{(G)[l]}\) 为
C和G在l层的激活,则有:$$J _{\text {content}}(C, G)=\dfrac {1}{2}||(a ^{(C)[l]}-a ^{(G)[l]})|| ^2$$\(a ^{(C)[l]}\) 和 \(a ^{(G)[l]}\)越相似,则 \(J _{\text {content}}(C, G)\) 越小。
风格代价函数
同一层的每个通道提取的特征不同(滤波器不同),例如有的通道提取垂直纹理特征,有的通道提取背景颜色。计算两个通道(同一层)间的相关性,即表示原始图片既包含了垂直纹理也包含了背景颜色的可能性大小。
通过 CNN ,风格被定义为同一个隐藏层不同通道之间激活值的相关系数,反映了原始图片特征之间的相互关系。
对于风格图像 S ,选择 l 层,则相关系数以一个 gram 矩阵形式表示:$$G _{kk’} ^{[l]\left (S\right )}=\sum _{i=1} ^{n _H ^{[l]}}\sum _{j=1} ^{n _W ^{[l]}}a _{ijk} ^{[l]\left (S\right )}a _{ijk’} ^{[l]\left (S\right )}$$其中 \(i\) 和 \(j\) 为 \(l\) 层的高度和宽度,\(k\) 和 \(k’\) 为选择的同一层的不同通道,范围为 \(1\) 到 \(n _C ^{[l]}\) ,\(a _{ijk} ^{[l]\left (S\right )}\) 为对应的激活值。同理对于生成图像 G 有:$$G _{kk’} ^{[l]\left (G\right )}=\sum _{i=1} ^{n _H ^{[l]}}\sum _{j=1} ^{n _W ^{[l]}}a _{ijk} ^{[l]\left (G\right )}a _{ijk’} ^{[l]\left (G\right )}$$则第 \(l\) 层的风格代价函数为:$$J _{\text {style}}^ {[l]}(S, G)=\dfrac {1}{(2n _H ^{[l]}n _W ^{[l]}n _C ^{[l]}) ^2}\sum _{k}\sum _{k’}(G _{kk’} ^{[l]\left (S\right )}-G _{kk’} ^{[l]\left (G\right )}) ^2$$对每一层都用风格代价函数,效果会更好,有:$$J _{\text {style}}(S, G)=\sum _{l}\lambda ^{[l]}J _{\text {style}}^ {[l]}(S, G)$$其中 \(\lambda \) 为设置不同层占的权重。
一维到三维推广
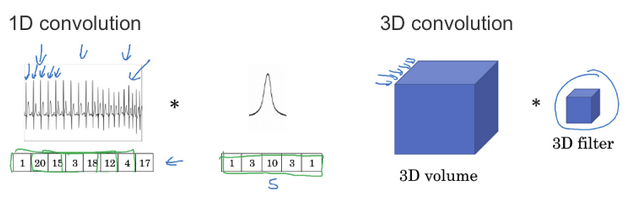
ECG 数据(心电图)是由时间序列对应的每个瞬间的电压组成,是一维数据。一般来说我们会用 RNN(循环神经网络)来处理,不过如果用卷积处理,则有:
- 输入时间序列维度:\(14\times 1\)
- 滤波器大小:\(5\times 1\) ,个数为 \(16\)
- 输出时间序列维度:\(10\times 16\)
对于三维图片有:
- 输入
3D图像大小:\(14\times 14\times 14\times 1\) - 滤波器大小:\(5\times 5\times 5\times 1\),个数为 \(16\)
- 输出
3D图片大小:\(10\times 10\times 10\times 16\)
相关连接:
DeepFace: Closing the gap to human-level performance in face verification
https://github.com/iwantooxxoox/Keras-OpenFace
TensorFlow Implementation of “A Neural Algorithm of Artistic Style”
MatConvNet
Very deep convolutional networks for large-scale image recognition
Convolutional neural networks for artistic style transfer
the official FaceNet github repository