拉格朗日数乘

Lagrange multipliers are used to find the stationary points of a function of several variables subject to one or more constrains.

等式限制的情况

考虑变量$\boldsymbol x\in R^{D}$，限制条件是$g(\boldsymbol x) = 0$。限制条件表示为在$\boldsymbol x$空间里的$D-1$维表面。在限制表面上的任何点，其梯度$\nabla g\left(\boldsymbol x\right)$都和限制表面正交。下图是对此说明。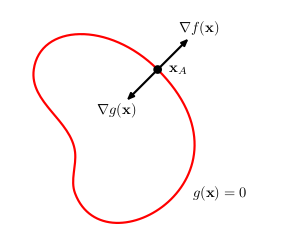
有等式约束的拉格朗日数乘图例

对上面一句话（其梯度$\nabla g\left(\boldsymbol x\right)$都和限制表面正交）证明:
考虑限制表面上的一个点$\boldsymbol x$，同时考虑一个相邻的点$\boldsymbol x+\boldsymbol \varepsilon$也在限制表面上，利用泰勒展开公式得到$$g\left(\boldsymbol x+\boldsymbol \varepsilon\right)=g\left(\boldsymbol x\right) +\boldsymbol \varepsilon^{T}\nabla g\left(\boldsymbol x\right)$$由于$\boldsymbol x$与$\boldsymbol x+\boldsymbol \varepsilon$都在限制表面上，得到$g(\boldsymbol x)=g(\boldsymbol x+\boldsymbol \varepsilon)$，因此有$\boldsymbol \varepsilon^{T}\nabla g\left(\boldsymbol x\right)=0$当$\lim \left| \boldsymbol \varepsilon\right| \rightarrow 0$。由于$\boldsymbol \varepsilon$和限制表面$g(\boldsymbol x) = 0$平行，所以梯度$\nabla g\left(\boldsymbol x\right)$都和限制表面正交。
杂谈：为什么有$\boldsymbol \varepsilon$和限制表面$g(\boldsymbol x) = 0$平行？

由于$\boldsymbol x$与$\boldsymbol x+\boldsymbol \varepsilon$都在限制表面上，说明向量$\boldsymbol \varepsilon$的”头”和”尾”都在限制表面上，因此有$\boldsymbol \varepsilon$和限制表面$g(\boldsymbol x) = 0$平行。

接下来的目的是要在限制表面$g(\boldsymbol x) = 0$上寻找一点$\boldsymbol x^\ast$，使得目标函数$f\left(\boldsymbol x\right)$取最大值。像这样的点满足一个属性：向量$\nabla f\left(\boldsymbol x\right)$也和限制表面正交。

如何理解向量$\nabla f\left(\boldsymbol x^\ast\right)$也和限制表面正交？
非正式的解释如下：$\boldsymbol x$在限制表面$g(\boldsymbol x) = 0$上移动，直到找到使目标函数$f\left(\boldsymbol x\right)$取最大值时停止，若$\nabla f\left(\boldsymbol x\right)$与$\nabla g\left(\boldsymbol x\right)$不共线，则$\nabla f\left(\boldsymbol x\right)$在该点有一个切向分量，$\boldsymbol x$沿着该分量移动使得$f\left(\boldsymbol x\right)$可以取得更大的值，最终会稳定在一个使得$\nabla f\left(\boldsymbol x\right)$与$\nabla g\left(\boldsymbol x\right)$共线的位置。（可以类比梯度法（上升/下降）找极值理解）

因此存在一个参数$\lambda$使得$$\nabla f\left(\boldsymbol x\right)+\lambda \nabla g\left(\boldsymbol x\right)=0$$进而自然引出拉格朗日函数$$L\left(\boldsymbol x,\lambda\right)=f\left(\boldsymbol x\right)+\lambda g\left(\boldsymbol x\right)$$通过令$\nabla _{\boldsymbol x}L=0$得到所求的极值点。(在等式限制条件下，$\min f(\boldsymbol x)$与$\max f(\boldsymbol x)$应用拉格朗日是对等的，没啥区别）

不等式限制条件

接下来探讨$\max f\left(\boldsymbol x\right)$，限制条件为$g\left(\boldsymbol x\right)\geq 0$，下图是对不等式约束情况说明。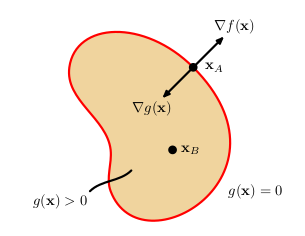
不等式约束的拉格朗日数乘法图例
针对不等式约束情况的解有两种情况：

落在$g(\boldsymbol x)>0$的区域。在此种情况下限制函数$g(\boldsymbol x)$不起作用，只需简单令$\nabla f(\boldsymbol x)=0$求解即可，这和等式限制条件下的拉格朗日函数中$\lambda =0$等价。
落在$g(\boldsymbol x)=0$的区域。这和之前讨论的等式约束条件类似，此时$\lambda \neq 0$。注意此时只有函数$f(\boldsymbol x)$的梯度$\nabla f\left(\boldsymbol x\right)$指向远离$g(\boldsymbol x)>0$的区域，才有函数$f(\boldsymbol x)$取极大值（上图有说明，解释可参考上面等式约束部分“非正式的解释”）。于是有$\nabla f(\boldsymbol x)=-\lambda\nabla g(\boldsymbol x)$，其中$\lambda >0$。

杂谈：如何确定限制面上的点的梯度$\nabla g(\boldsymbol x)$的指向（图中示例都是指向限制面包裹区域的内部)

梯度：函数在某一点的梯度是这样一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。沿梯度方向，函数值增加最快（此时方向导数是正值，取最大），为更好理解考虑下面用泰勒公式展开的一元函数$$f(x+\nabla x)\approx f(x)+f’(x)\nabla x$$当$f’(x)>0$时，函数值增加。当$f’(x)<0$时，函数值减小，多元函数类似。
回归正题：由刚才的分析可知，沿梯度的方向，函数值增加最快，因此可得到梯度的方向就是函数值增加的方向。由于上面图给出$g(\boldsymbol x)>0$在内部，因此梯度方向也就指向内部了。（若$g(\boldsymbol x)>0$在外部，那梯度方向就指向外部了，之前的所有分析都是还成立的）

以上两种情况都有$\lambda g(\boldsymbol x)=0$，因此问题转为下式带约束的极大值$$L\left(\boldsymbol x,\lambda\right)=f\left(\boldsymbol x\right)+\lambda g\left(\boldsymbol x\right)$$$$s.t.\begin{cases}g\left( x\right) =0\\ \lambda \geq 0\\ \lambda g\left( x\right) =0\end{cases}$$约束条件为KKT条件。
注意如果是$\min f\left(\boldsymbol x\right)$，限制条件为$g\left(\boldsymbol x\right)\geq 0$，则拉格朗日函数应该为$L\left(\boldsymbol x,\lambda\right)=f\left(\boldsymbol x\right)-\lambda g\left(\boldsymbol x\right)$其中$\lambda \geq 0$

对上面注意事项解释如下
如果限制条件成立，则$L(\boldsymbol x,\lambda)=f(\boldsymbol x)$;但是若限制条件不满足，即$g(\boldsymbol x)<0$，则需要惩罚，由于$\lambda\geq 0$则惩罚项$\lambda g(\boldsymbol x)=-\infty$。则$L(\boldsymbol x,\lambda)=f(\boldsymbol x)-(-\infty)$，因此问题转为$$L\left(\boldsymbol x,\lambda\right) =\begin{cases}f\left( x\right) ,满足限制\\ +\infty ,不满足限制\end{cases}$$在这种情况下最小化才有意义（和原文题$\min f\left(\boldsymbol x\right)$保持一致）。如果拉格朗日数乘算子前还是”+”的话，则问题转为$$L\left(\boldsymbol x,\lambda\right) =\begin{cases}f\left( x\right) ,满足限制\\ -\infty ,不满足限制\end{cases}$$此时最小化无意义。（此思想对于其他的情况也适用）

将上述等式约束和不等式约束组合可得到拉格朗日数乘公式的一般形式，具体就不写了，注意KKT条件。

参考:PRML
结束