最长回文

最长回文子串

题目：给定一个字符串\(s\)，找到\(s\)中最长回文子串
输入：babad
输出：bab或者aba

动态规划解
在验证一个子串是不是回文时候，应该避免不必要的重复验证计算。以ababa为例，如果已经知道bab是回文，则ababa一定是回文，因为子串首和尾是相同的a。有如下定义$$P(i, j) = \begin{cases}\text{true}, \quad &\text{如果子串\(s_i\dots s_j\)是回文}\\ \text{false}, \quad &\text{其它}\end{cases}$$进而有如下的递推公式$$\begin{cases}P(i, j) = \Big(P(i+1, j-1) \quad \text{and} \quad s_i == s_j\Big)\\P(i,i)=\text{true}\\P(i,i+1)=(s_i==s_j)\end{cases}$$需要一个\(n\times n\)的表table，其中\(\text{table}[i, j] = P(i, j), \quad i \le j\)。以babad为例，下图是table示意图，按照对角线顺序（左上角到右下角），依次从主对角线开始，沿着右上方向，依次填充，直到右顶点（或者从下往上，一层一层（水平方向）填充）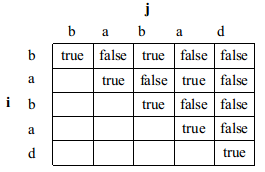
时间复杂度为\(O(n^2)\)，空间复杂度为\(O(n^2)\)

C++实现

string longestPalindrome(string s) {
    int n = s.size();
    if(n <= 0) return "";
    if(n == 1) return s;
    //vector<vector<bool>> table(n, vector<bool>(n, false)); // 花费更多的时间和空间：216ms 和 18.9MB
    bool table[1000][1000] = {false}; // 64ms 和 9.9MB
    int maxLength = 1;
    int old_i = 0;
    for(int i = 0; i < n-1; ++i)
    {
        table[i][i] = true;
        if(s[i+1] == s[i])
        {
            table[i][i+1] = true;
            old_i = i;
            maxLength = 2;
        }
    }
    table[n-1][n-1] = true;
    for(int l = 2; l < n; ++l)
    {
        for(int i = 0; i < n - l; ++i)
        {
            int j = i + l;
            if(table[i+1][j-1] && s[i] == s[j])
            {
                table[i][j] = true;
                old_i = i;
                maxLength = j - i + 1;
            }
        }
    }
    return s.substr(old_i, maxLength);
}

运行时间：\(64\text{ms}\) 超过\(46.24\%\); 内存：\(9.9\text{MB}\) 少于\(54.48\%\)
中心拓展解
根据观察可知，回文子串是关于其中心镜像对称。因此，一个回文可以从其中心向两边拓展。长度为\(\text{n}\)的字符串，有\(2\text{n}-1\)个中心，因为一个回文的中心可以在两个字符之间（偶数个字符），例如bb是一个回文，其中心在两个字符中间。下图是中心拓展示意图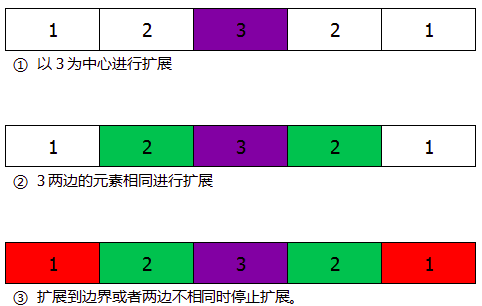
时间复杂度为\(O(n^2)\)，空间复杂度为\(O(1)\)

C++实现

class Solution {
public:
    string longestPalindrome(string& s) {
        const int n = s.size();
        if(n <= 0) return "";
        int start = 0, end = 0;
        for(int i = 0; i < n; ++i)
        {
            int len1 = expandAroundCenter(s, i, i); // 以第i个字符为中心
            int len2 = expandAroundCenter(s, i, i+1); // 以第i个字符和第i+1个字符为中心
            int len = len1 > len2 ? len1 : len2;
            if(len > end - start)
            {
                start = i - ((len - 1) >> 1); // 位移符号优先级低于四则运算符号
                end = i + (len >> 1);
            }
        }
        return s.substr(start, end - start + 1);
    }
private:
    int expandAroundCenter(string& s, int left, int right)
    {
        while(left >= 0 && right < s.size() && s[left] == s[right])
        {
            left--;
            right++;
        }
        return right - left - 1; // 回文的长度
    }
};

运行时间：\(24\text{ms}\) 超过\(67.36\%\); 内存：\(8.7\text{MB}\) 少于\(92.41\%\)
Manacher’s Algorithm
Manacher 算法首先对字符串预处理，在所有空位置（包括首尾）插入同样的符号，且要求这个符号在原串中没有出现。则会使得原串长度是奇数，以插入#为例$$\begin{aligned}aba &\rightarrow \# a\# b\# a\# \\ abba &\rightarrow \# a\# b\# b\# a\#\end{aligned}$$由于插入是同样符号，且插入符号不在原串中，因此原串的回文性不会受到影响
称一个回文串的最左或者最右字符与其对称轴的距离为回文半径，Manacher算法定义一个回文半径数组\(RL[i]\)表示以第\(i\)个字符为对称轴的回文串的回文半径$$\begin{equation}\begin{aligned}
\text{char}&:\quad &\# \quad &a \quad &\# \quad &b \quad &\# \quad &a \quad &\#\\
\text{RL}&:\quad &1 \quad &2 \quad &1 \quad &4 \quad &1 \quad &2 \quad &1\\
\text{RL-1}&:\quad &0 \quad &1 \quad &0 \quad &3 \quad &0 \quad &1 \quad &0\\
\text{i}&:\quad &0 \quad &1 \quad &2 \quad &3 \quad &4 \quad &5 \quad &6
\end{aligned}\end{equation}$$观测可知，\(R[i]-1\)是所求回文的串的长度，问题变为求\(RL[i]\)数组。引入一个辅助变量maxRight表示当前能访问到的回文子串中，最靠右的字符位置，同时需要记录maxRight对应的回文串对称轴位置pos，如下图所示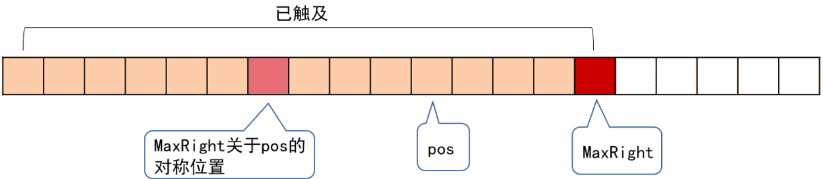从左到右依次访问字符串求\(RL[i]\)数组。假设当前\(RL[pos]\)已知，需要求下一个位置\(i\)，下面分两种情况讨论

1. 当\(i\)在maxRight的左边时候，如下图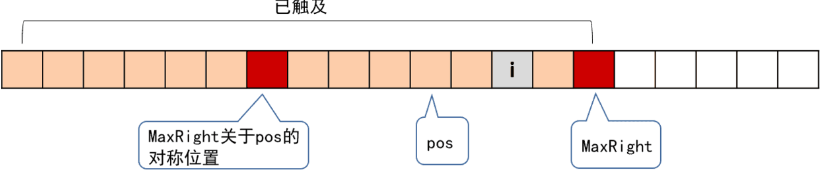图中红色块之间（包括）串是回文的，以\(i\)为对称轴的回文串与红色块之间有重叠。可以找到\(i\)关于pos的对称位置\(j\)，其中\(RL[j]\)已经计算过，根据对称性，以\(i\)为对称轴的回文串和以\(j\)为对称轴的回文串有部分相同
   当以\(j\)为对称轴回文串较短时候，如下图有\(RL[i] \ge RL[j]\)，令\(RL[i] = RL[j]\)，同时试着以\(i\)为对称轴，向两边拓展，知道左右字符不同或者到达边界，更新maxRight和pos
   当以\(j\)为对称轴回文串较长时候，如下图只能确定在蓝色虚线之间是回文的（不超过maxRight)，同时从这个长度开始，试着以\(i\)为对称轴，向两边拓展，知道左右字符不同或者到达边界，更新maxRight和pos
2. 当\(i\)在maxRight的右边时候，如下图以\(i\)为对称轴，向两边拓展，知道左右字符不同或者到达边界，更新maxRight和pos

时间复杂度\(O(n)\)，空间复杂度\(O(n)\)

C++实现

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        if(n < 2) return s;
        string str = "";
        for(int i = 0; i < n; ++i)
        {
            str.push_back('#');
            str.push_back(s[i]);
        }
        str.push_back('#');
        n = str.size();
        int* RL = new int[n];
        int maxRight = 0, maxLen = 0, pos = 0, start=0;
        for(int i = 0; i < n; ++i)
        {
            if(i < maxRight)
                RL[i] = RL[(pos<<1) - i] < maxRight -i ? RL[(pos << 1) - i] : maxRight - i;
            else
                RL[i] = 1;
            while(i - RL[i] >= 0 && i + RL[i] < n && str[i-RL[i]] == str[i+RL[i]]) // 向两边拓展
                RL[i] += 1;
            if(RL[i] + i - 1 > maxRight)
            {
                maxRight = RL[i] + i - 1;
                pos = i;
            }
            if(maxLen < RL[i])
            {
                start = i;
                maxLen = RL[i];
            }
        }
        int p = (start - maxLen + 1) >> 1;
        return s.substr(p, maxLen-1);
    }
};

运行时间：\(8\text{ms}\) 超过\(90.72\%\); 内存：\(9.9\text{MB}\) 少于\(54.48\%\)

最长回文子序列

题目：给定一个字符串\(s\)，找到\(s\)中最长回文子序列
输入：bbbab
输出：4(bbbb)

动态规划解
对于任意字符串，如果头尾字符相同，那么字符串的最长子序列等于去掉首尾的字符串的最长子序列加上首尾；如果首尾字符不同，则最长子序列等于去掉头的字符串的最长子序列和去掉尾的字符串的最长子序列的较大者，定义\(c[i, j]\)表示字符串\(s_i\dots s_j\)的最长回文子序列\(i\le j\)，则有如下状态转移方程$$\begin{equation}c[i, j] = \begin{cases}1, \quad i==j \\
0, \quad i > j\\
\text{max}(c[i+1, j], c[i, j-1]), \quad s[i]\not = s[j]\\
c[i+1, j-1] + 2, \quad s[i] == s[j]
\end{cases}\end{equation}$$从下往上，一层一层（水平方向）填充
时间复杂度为\(O(n^2)\)，空间复杂度为\(O(n^2)\)

C++实现

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        if(n < 1) return 0;
        if(n == 1) return 1;
        int table[1000][1000] = {0};
        for(int i = 0; i < n; ++i)
        {
            table[i][i] = 1;
        }
        for(int i = n-2; i >= 0; --i)
        {
            for(int j = i+1; j < n; ++j)
            {
                if(s[i] == s[j])
                    table[i][j] = table[i+1][j-1] + 2;
                else
                    table[i][j] = table[i+1][j] > table[i][j-1] ? table[i+1][j] : table[i][j-1];
            }
        }
        return table[0][n-1];
    }
};

运行时间：\(52\text{ms}\) 超过\(90.06\%\); 内存：\(12.3\text{MB}\) 少于\(100.00\%\)

参考：Manacher 算法