前缀树介绍
一种多叉树结构,数据(键)不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,根节点对应空字符串。通常在实现的时候,会在节点结构中设置一个标志,用来标记该结点处是否构成一个单词(关键字),下图是前缀树例子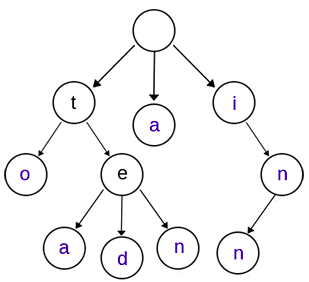 表示了关键字集合{“a”, “to”, “tea”, “ted”, “ten”, “i”, “in”, “inn”}
表示了关键字集合{“a”, “to”, “tea”, “ted”, “ten”, “i”, “in”, “inn”}
前缀树结构特点
- 根节点一般为空
- 每个节点最多有R个孩子,每个孩子分别对应字母表数据集中的一个字母(通常情况下R为26,表示有26个英文字母)
- 每个节点有一个标志,表示当前节点是不是关键字的结束
插入操作
从根节点开始,向下依次寻找当前节点的link(存放孩子节点的指针)中,是否有与关键字key中相应位置字母相同的link:
- 如果有:沿着该link向下一层继续寻找
- 如果没有:新建一个node,插入当前节点的link中,继续向下寻找
遍历到key的末尾时,修改该节点的标志,指示关键字的末尾
查找操作
从根节点开始,根据关键字key中的字母依次验证不同的link向下寻找,依次比较当前节点link中是否有和关键字相应字母相同的link:
- 如果有:继续到下一层
- 如果没有:看关键字是否遍历到了末尾,如果到了末尾的话, 说明匹配成功; 如果没有到末尾,说明只匹配到了关键字的一个前缀,匹配失败
查找是否是前缀
与查找操作相似,不同的是, 这里的关键字不必是某个单词的末尾, 只需是前缀即可
C++ 实现
1 | // 树节点类,由两部分组成 |
优点与应用
trie优于哈希表的一个原因是,随着哈希表的大小增加,会有很多哈希冲突,搜索时间复杂度可能会恶化到 O(n),当存储具有相同前缀的多个关键字时,Trie可以使用比哈希表少的空间
使用trie只有O(m)时间复杂度,在平衡树中查找关键字的时间复杂度为O(mlogn)
应用
- 字符串检索
- 词频统计:修改了节点结构,用一个整型变量count来计数。对每一个关键字执行插入操作,若已存在,计数加1,若不存在,插入后count置1
- 字符串排序:遍历一次所有关键字,将它们全部插入trie树,树的每个结点的所有儿子很显然地按照字母表排序,然后先序遍历输出Trie树中所有关键字即可
- 前缀匹配:例如,找出一个字符串集合中所有以ab开头的字符串,我们只需要用所有字符串构造一个trie树,然后输出以a->b->开头的路径上的关键字即可。前缀匹配常用于搜索提示