动态规划
动态规划(dynamic programming)与分治算法相似，都是通过组合子问题的解来求解原问题（这里
programming指的是一种表格法）。分治算法将问题划分为互不相交的子问题，递归求解子问题，再将它们的解组合起来，求出原问题的解。与之相反，动态规划应用于子问题重叠的情况，即不同子问题具有公共的子子问题（子问题的求解是递归的，将其划为更小的子子问题），在这种情况下，分治算法会做许多不必要的工作，即它会反复求解那些公共的子子问题。而动态规划算法对每个子子问题只求解一次，将其解保存在一个表格中，从而无需每次求解一个子子问题都重新计算，避免不必要的工作
钢条切割问题
问题：给定一段长度为\(n\)的钢条和一个价格表\(p_i(i=1, 2, \dots, n)\)，求切割方案使得销售收益\(r_n\)最大（可以不切割）。例如有如下的价格表
| 长度\(i\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 价格\(p_i\) | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
考虑\(n=4\)，下图给出所有的可能切割方案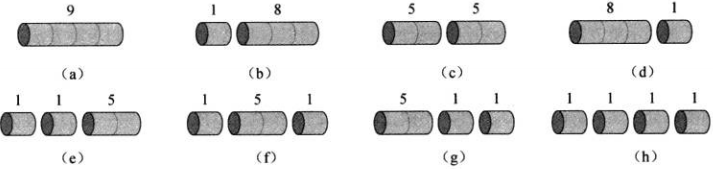
有\(p_2 + p_2 = 5 + 5 = 10\)的最优解。长度为\(n\)的钢条有\(2^{n-1}\)种切割方案，因为距离钢条左端\(i(i=1, 2, \dots, n-1)\)处有切或者不切两种选择
自顶向下的递归解
将钢条从左边切割下长度为\(i\)的一段，只对右边剩下的\(n-i\)的一段继续进行切割（递归求解），对左边不再进行切割。可以得到递归方程如下$$r_n=\mathop{\text{max}}\limits_{1\le i\le n}(p_i + r_{n-i})$$原问题的最优解只包含一个相关子问题的解，而不是两个。相关的伪代码如下1
2
3
4
5
6
7CUT-ROD(p, n)
if n == 0
return 0
q = -infty
for i = 1 to n
q = max(q, p[i]+CUT-ROD(p, n-i))
return q
时间复杂度$$T(n)=1+\sum_{j=0}^{n-1}T(j)$$其中\(T(0)=1\)，\(j=n-i\)，可以证明$$T(n)=2^n$$
C++实现（递归实现）
1 |
|
输入规模稍微增大，运行时间会变得很长，原因是递归会反复求解相同的子问题
动态规划求解最优切割
递归方法之所以低效，是因为它反复求解相同的子问题。因此，动态规划仔细安排求解顺序，对每个子问题只求解一次，将结果保存下来，之后再需要此子问题的解，只需要查找保存的结果即可，是典型的时间换空间
带备忘的自顶向下法(top-down with memoization)–递归
此方法依然按照递归的形式编写，但过程中会保存每个子问题的解（保存在一个数组或者散列表中）。当需要一个子问题的解时，首先检查是否已经保存过此解，如果是这直接返回保存结果；否则，按照通常方式计算这个子问题，称这个递归过程是带备忘的
自顶向下伪代码如下（加入备忘机制）1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17MEMOIZED-CUT-ROD(p, n)
let r[0...n] be a new array
for i = 0 to n
r[i] = -infty
return MEMOIZED-CUT-ROD-AUX(p, n, r)
MEMOIZED-CUT-ROD-AUX(p, n, r)
if r[n] >= 0
return r[n]
if n == 0
q = 0
else
q = -infty
for i = 1 to n
q = max(q, p[i] + MEMOIZED-CUT-ROD-AUX(p, n-i, r))
r[n] = q
return q
时间复杂度为\(O(n^2)\)
C++实现（自顶向下-带备忘录）–递归实现
1 |
|
自底向上法(bottom-up method)–迭代
这一方法需要恰当定义子问题规模，使得任何子问题的求解都依赖于更小子问题的求解，因而，可以将子问题按照规模，由小到大顺序求解。当求解某个子问题时，其所依赖的更小的子问题都已经求解完毕。每个子问题只求解一次
自底向上的伪代码如下1
2
3
4
5
6
7
8
9BOTTOM-UP-CUT-ROD(p, n)
let r[0...n] be a new array
r[0] = 0
for j = 1 to n
q = -infty
for i = 1 to j
q = max(1, p[i] + r[j-i])
r[j] = q
return r[n]
采用子问题的自然顺序，若\(i < j\)，则规模为\(i\)的子问题比规模为\(j\)的子问题更小，因此依次求解规模为\(j=0, 1, 2, \dots, n\)的子问题
时间复杂度为\(O(n^2)\)
C++实现（自底向上）–迭代实现
1 |
|
两种方法的渐进时间复杂度一样，但是由于没有频繁的递归调用，自底向上的方法时间复杂度通常有更小的系数
子问题图
当考虑动态规划问题时，应该考虑子问题和子问题之间的关系，下图是切割钢条问题中\(n=4\)的子问题图，每一个节点表示一个子问题，有向边表示子问题和子问题之间的关系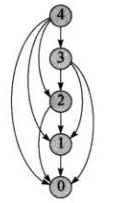
一个子问题的求解时间与子问题图中对应顶点的出射边数成正比，子问题的数目等于子问题图的顶点数。通常情况下，动态规划算法运行时间与顶点和边的数量成线性关系
重构解
之前讨论的动态规划算法只是返回最优解值，并没有返回解本身（即长度列表，给出切割后每段长度），可以拓展动态规划算法，使之对每个子问题不仅保存最优值，还保存切割方案。下面给出自底向上动态规划算法BOTTOM-UP-CUT-ROD的拓展版本，对长度为\(j\)的钢条不仅保存最优值\(r_j\)，还保存最优解对应的第一段钢条的切割长度\(s_j\)1
2
3
4
5
6
7
8
9
10
11EXTENDED-BOTTOM-UP-CUT-ROD(p, n)
let r[0...n] and s[0...n] be new arrays
r[0] = 0
for j = 1 to n
q = -infty
for i = 1 to j
if q < p[i] + r[j-i]
q = p[i] + r[j-i]
s[j] = i
r[j] = q
return r and s
C++实现（自底向上拓展版本）
1 |
|
最长公共子序列(LCS)
问题：给定两个序列\(X=<x_1, x_2, \dots, x_m>\)和\(Y=<y_1, y_2, \dots, y_n>\)，求\(X\)和\(Y\)的最长公共子序列（注：子序列在\(X\)和\(Y\)中不要求连续出现）
考虑序列\(X\)的长度为\(m\)，则\(X\)共有\(2^m\)个子序列（每个位置有选或者不选两种状态），暴力解法（穷举所有）时间复杂度是指数阶，在实际中不实用
LCS的最优子结构：令\(X=<x_1, x_2, \dots, x_m>\)和\(Y=<y_1, y_2, \dots, y_n>\)为两个序列，\(Z=<z_1, z_2, \dots, z_k>\)为\(X\)和\(Y\)的任意LCS
- 如果\(x_m = y_n\)，则\(z_k = x_m = y_n\)且\(Z_{k-1}\)是\(X_{m-1}\)和\(Y_{n-1}\)的一个LCS
- 如果\(x_m \not = y_n\)，那么\(z_k \not = x_m\)意味着\(Z\)是\(X_{m-1}\)和\(Y\)的一个LCS
- 如果\(x_m \not = y_n\)，那么\(z_k \not = y_n\)意味着\(Z\)是\(X\)和\(Y_{n-1}\)的一个LCS
其中定义\(X\)的第\(i\)个前缀为\(X_i=<x_1, x_2, \dots, x_i>\)
一个递归解
根据LCS的最优子结构，我们需要求解一个或两个子问题。如果\(x_m = y_n\)，我们应该求解\(X_{m-1}\)和\(Y_{n-1}\)的一个LCS，将\(x_m = y_n\)追加到这个LCS的结尾，就得到\(X\)和\(Y\)的一个LCS。如果\(x_m \not = y_n\)，需要求解两个子问题：求\(X_{m-1}\)和\(Y\)的一个LCS与\(X\)和\(Y_{n-1}\)的一个LCS，比较两个LCS中的较长者为最终结果。可以较容易看出重叠子问题的性质，为了求解\(X\)和\(Y\)的一个LCS，可能需要求\(X_{m-1}\)和\(Y\)的一个LCS与\(X\)和\(Y_{n-1}\)的一个LCS，但这几个子问题都包含求解\(X_{m-1}\)和\(Y_{n-1}\)的LCS子子问题，很多其他子问题也都有共享子子问题
我们定义\(c[i, j]\)表示\(X_i\)和\(Y_j\)的LCS长度。如果\(i=0\)或者\(j=0\)，即一个序列长度为\(0\)，那么LCS的长度为\(0\)，有如下递归方程$$\begin{equation}
c[i, j] = \begin{cases}0, &\text{若}i=0\text{或}j=0\\
c[i-1, j-1], &\text{若}i, j > 0\text{且}x_i = y_j\\
\text{max}(c[i, j-1], c[i-1, j]), &\text{若}i, j > 0\text{且}x_i \not = y_j
\end{cases}\end{equation}$$根据此递归公式可以容易写出一个指数时间的递归算法
动态规划解
由于LCS只有\(O(mn)\)个不同子问题（每一个子问题都是对应输入序列的某个前缀，序列\(X\)前缀长度有\(1, 2, \dots, m\)，共\(m\)种；序列\(Y\)前缀长度有\(1, 2, \dots, n\)，共\(n\)种，因此共有\(mn\)个子问题），因此可以用动态规划求解，期望时间复杂度为\(O(mn)\)
过程LCS-LENGTH接收两个序列\(X=<x_1, x_2, \dots, x_m>\)和\(Y=<y_1, y_2, \dots, y_n>\)作为输入。将\(c[i, j]\)的值保存在表\(c[0…m, 0…n]\)中，按照行主次序计算表项（首先由左至右计算\(c\)的第一行，然后计算第二行，以此类推）。过程中还维护一个表\(b[1…m, 1…n]\)，帮助构造最优解。\(b[i, j]\)指向的表项对应计算\(c[i, j]\)时选择的子问题最优解。返回表\(b\)和表\(c\)，其中\(c[m, n]\)保存了\(X\)和\(Y\)的LCS值
伪代码如下（其中\(\text{nw} = \nwarrow, \quad \text{up} = \uparrow, \quad \text{left} = \leftarrow\)）1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20LCS-LENGTH(X, Y)
m = X.length
n = Y.length
let b[1...m, 1...n] and c[0...m, 0...n] be new tables
for i = 1 to m
c[i, 0] = 0
for j = 0 to n
c[0, j] = 0
for i = 1 to m
for j = 1 to n
if x_i == y_j
c[i, j] = c[i-1, j-1] + 1
b[i, j] = "nw"
elseif c[i-1, j] >= c[i, j-1]
c[i, j] = c[i-1, j]
b[i, j] = "up"
else
c[i, j] == c[i, j-1]
b[i, j] = "left"
return c and b
下图显示了LCS-LENGTH对输入序列\(X=<A, B, C, B, D, A, B>\)和\(Y=<B, D, C, A, B, A>\)生成的结果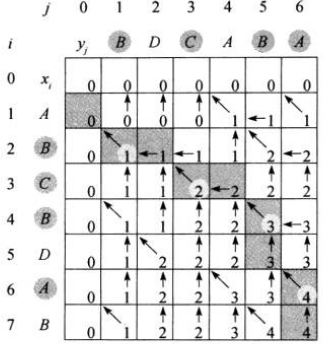
时间复杂度为\(O(mn)\)，每个表项的计算时间是\(O(1)\)
根据LCS-LENGTH返回的\(\text{b}\)，可快速构造\(X\)和\(Y\)的LCS，只需要从\(b[m,n]\)开始，按照箭头方向追踪即可，时间复杂度为\(O(m+n)\)1
2
3
4
5
6
7
8
9
10PRINT-LCS(b, X, i, j)
if(i == 0 or j == 0)
return
if b[i, j] == "nw"
PRINT-LCS(b, X, i-1, j-1)
print x_i
elseif b[i, j] == "up"
PRINT-LCS(b, X, i-1, j)
else
PRINT-LCS(b, X, i, j-1)
C++实现（自底向上）
1 |
|
最优二叉搜索树
背景：假设设计一个程序，实现英语到法语的翻译。对英语文本中的每个单词，需要查找对应的法语单词。为了实现这样的查找操作，可以创建一个二叉搜索树，将\(n\)个英语单词作为关键字，对应的法语单词作为关联的数据。由于对文本中的每个单词需要搜索，希望花费在搜索上的时间尽可能少。通过使用红黑树或者其他平衡搜索树，可以假定每次搜索时间为\(O(\lg n)\)。但是，每个单词出现的频率是不同的，例如“the”这样频繁使用的单词可能会位于搜索树中远离树根的位置，而“machicolation”这种很少使用的单词可能位于靠近根的位置上，这样会减慢翻译的速度，因为在二叉搜索树中搜索一个关键字需要访问的节点数等于包含关键字的节点深度加\(1\)。希望频繁出现的单词出现在靠近根的位置。同时，文本中的一些单词可能没有对应的法语单词，这些单词不应该出现在二叉搜索树中。在给定单词出现频率的前提下，应该如何组织二叉搜索树，使得搜索操作访问的总节点数最少的问题称为最优二叉搜索树
问题定义如下：给定一个\(n\)个不同关键字的已排序的序列\(K=<k_1, k_2, \dots, k_n>\)(\(k_1 < k_2 < \dots < k_n\))，希望用这些关键字构造二叉搜索树，对于每个关键字\(k_i\)，都有一个概率\(p_i\)表示其搜索频率。有些搜索值可能不在\(K\)中，因此还有\(n+1\)个伪关键字\(d_0, d_1, \dots, d_n\)表示不在\(K\)中的值。对于每个伪关键字\(d_i\)，也有一个概率\(q_i\)表示对应的搜索频率。下图表示\(n=5\)时构造的两颗二叉搜索树，其中每个关键字\(k_i\)是一个内部节点，每个伪关键字是一个叶节点。每次搜索要么成功（找到关键字\(k_i\)），要么失败（找到某个伪关键字\(d_i\)），有如下公式$$\sum_{i=1}^{n}p_i + \sum_{i=0}^{n}q_i = 1$$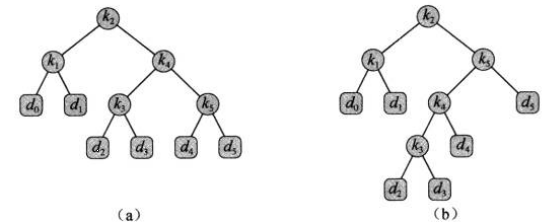
各个节点对应搜索频率如下表
| \(i\) | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| \(p_i\) | 0.15 | 0.10 | 0.05 | 0.10 | 0.20 | |
| \(q_i\) | 0.05 | 0.10 | 0.05 | 0.05 | 0.05 | 0.10 |
则\(a\)中期望搜索代价为\(2.80\)，\(b\)期望搜索代价为\(2.75\)（最优）
假设一次搜索的代价等于访问的节点数，即此次搜索找到的节点在\(T\)中的深度加\(1\)，那么在\(T\)中进行一次搜索的期望代价为$$\begin{equation}\begin{aligned}E[\text{T中搜索代价}] &= \sum_{i=1}^{n}(\text{depth}_T (k_i) + 1)\times p_i + \sum_{i=0}^{n}(\text{depth}_T (d_i) + 1) \times q_i \\ &=1 + \sum_{i=1}^{n}\text{depth}_T (k_i)\times p_i + \sum_{i=0}^{n}\text{depth}_T (d_i) \times q_i\end{aligned}\end{equation}$$其中\(\text{depth}_T\)表示一个节点在\(T\)中的深度。对于上图\(a\)，有如下计算代价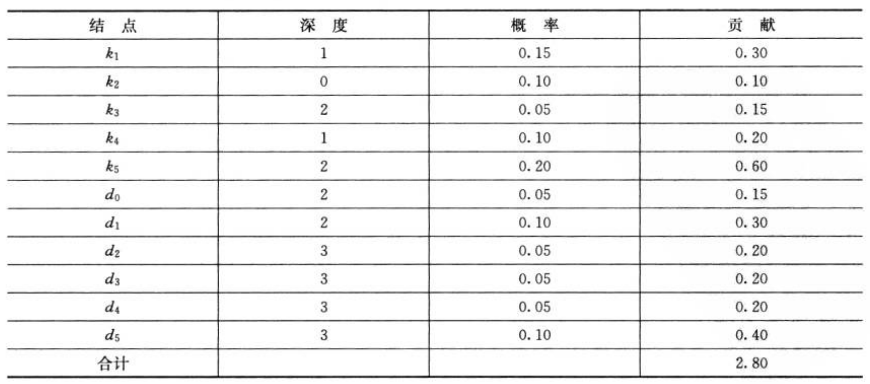
最优二叉搜索树不一定是高度最矮，且频率最高的关键字不一定出现在树的根节点上，如上图\(b\)
最优子结构
考虑一颗二叉搜索树的任意子树，它必须包含连续关键字\(k_i, \dots, k_j, \quad 1 \le i \le j \le n\)，且其叶节点必然是伪关键字\(d_{i-1}, \dots, d_j\)。如果一颗最优二叉搜索树\(T\)有一颗包含关键字\(k_i, \dots, k_j\)的子树\(T’\)，那么\(T’\)必然是包含关键字\(k_i, \dots, k_j\)和伪关键字\(d_{i-1}, \dots, d_j\)的子问题的最优解。可以用剪切粘贴证明：如果存在子树\(T’’\)，其期望搜索代价比\(T’\)低，则可以将\(T’\)从\(T\)中删除，将\(T’’\)粘贴到相应的位置，从而得到一颗期望搜索代价更低的树\(T\)，其与\(T\)假设是最优的矛盾。
用子问题的最优解来构造原问题的最优解。给定关键字序列\(k_i, \dots, k_j\)，其中某个关键字\(k_r(i\le r\le j)\)作为这些关键字的最优子树的根节点。那么\(k_r\)的左子树包含关键字\(k_i, \dots, k_{r-1}\)（和伪关键字\(d_{i-1}, \dots, d_{r-1}\)），右子树包含关键字\(k_{r+1}, \dots, k_j\)（和伪关键字\(d_r, \dots, d_j\)）。对所有可能的根节点\(k_r\)，并对每种情况分别求解包含\(k_i, \dots, k_{r-1}\)及包含\(k_{r+1}, \dots, k_j\)的最优二叉搜索树，即可保证找到原问题最优解。
还需要注意一个细节–空子树。假设对包含关键字\(k_i, \dots, k_j\)的子问题，选择\(k_i\)为根节点，则其左子树为空，但是依然包含伪关键字\(d_{i-1}\)。对称地，如果选择\(k_j\)为根节点，则右字树为空，但是依然包含伪关键字\(d_j\)
递归解
选取子问题域为：求解包含关键字\(k_i, \dots, k_j\)的最优二叉搜索树，其中\(i\ge 1, j\le n\)且\(j\ge i-1\)（当\(j=i-1\)时，子树为空，只有伪关键字\(d_{i-1}\)）。定义\(e[i, j]\)为包含关键字\(k_i, \dots, k_j\)的最优二叉搜索树中进行一次搜索期望代价，最终希望计算出\(e[1, n]\)
当\(j=i-1\)的情况最为简单，由于子树只包含伪关键字\(d_{i-1}\)，期望搜索代价是\(e[i, i-1]=q_{i-1}\)
当\(j\ge i\)时，需要从关键字\(k_i, \dots, k_j\)中选择一个根节点\(k_r\)，构造一颗包含关键字\(k_i, \dots, k_{r-1}\)作为左子树，及包含关键字\(k_{r+1}, \dots, k_j\)作为右子树。当一颗子树成为一个节点的子树时，由于每个节点的深度增加\(1\)，因此根据上面期望代价公式，这颗子树的期望搜索代价增加值为所有节点概率之和，即$$\omega(i, j) = \sum_{l=i}^{j}p_l + \sum_{l=i-1}^{j}q_l$$因此，若\(k_r\)为包含关键字\(k_i, \dots, k_j\)的最优二叉搜索树的根节点，有如下公式$$e[i, j]=p_r + (e[i, r-1] + \omega(i, r-1)) + (e[r+1, j] + \omega(r+1, j))$$注意\(\omega(i, j) = \omega(i, r-1) + p_r + \omega(r+1, j)\)，因此\(e[i, j]\)可重写为$$e[i, j] = e[i, r-1] + e[r+1, j] + \omega(i, j)$$则有如下的递推公式$$e[i, j] = \begin{cases}q_{i-1} \quad &\text{若}j=i-1\\ \mathop{\text{min}}\limits_{i\le r\le j}\{e[i, r-1] + e[r+1, j] + \omega(i, j)\} \quad &\text{若}i\le j\end{cases}$$\(e[i, j]\)的值给出最优二叉搜索树的期望代价。为了记录最优二叉搜索树的结构，对于包含关键字\(k_i, \dots, k_j, \quad 1\le i\le j\le n\)的最优二叉搜索树，定义\(\text{root}[i, j]\)保存根节点\(k_r\)的下标\(r\)
动态规划解
我们用一个表\(e[1…n+1, 0…n]\)保存\(e[i, j]\)的值。第一维下标上界为\(n+1\)而不是\(n\)，原因在于对于只包含伪关键字\(d_n\)的子树，需要计算并保存\(e[n+1, n]\)。第二维下标为\(0\)开始，因为对于伪关键字\(d_0\)，需要计算并保存\(e[1, 0]\)。只使用表中满足\(j\ge i-1\)的表项\(e[i, j]\)。还需要使用一个表\(\text{root}\)，表项\(\text{root}[i, j]\)，记录包含关键字\(k_i, \dots, k_j\)的子树的根。只使用表中满足\(1\le i\le j\le n\)的项。还需要使用另一个表\(\omega[1…n+1, 0…n]\)，为了避免每次计算\(e[i, j]\)时，都要重新计算\(\omega[i, j]\)。每次可以节省\(O(j-i)\)次加法。对于基本情况，令\(\omega[i, i-1]=q_{i-1}(1\le i\le n+1)\)，对于\(j\ge i\)的情况，通过如下计算$$\omega[i, j]=\omega[i, j-1] + p_j + q_j$$增加一个节点\(j\)，则对比之前，多引入一个节点及一个伪节点，则期望搜索代价增加\(p_j + q_j\)
伪代码如下，接收概率列表\(p_1, p_2, \dots, p_n\)和\(q_0, q_1, \dots, q_n\)及规模\(n\)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16OPTIMAL-BST(p, q, n)
let e[1...n+1, 0...n], w[1...n+1, 0...n] and root[1...n, 1...n] be new arrays
for i=1 to n+1
e[i, i-1] = q_{i-1}
w[i, i-1] = q_{i-1}
for l=1 to n
for i = 1 to n-l+1
j = i+l-1
e[i, j] = infty
w[i, j] = w[i, j-1] + p_j + q_j
for r = i to j
t = e[i, r-1] + e[r+1, j] + w[i, j]
if(t < e[i, j])
e[i, j] = t
root[i, j] = r
return e and root
时间复杂度为\(O(n^3)\)。下图是输入上述例子频率值结果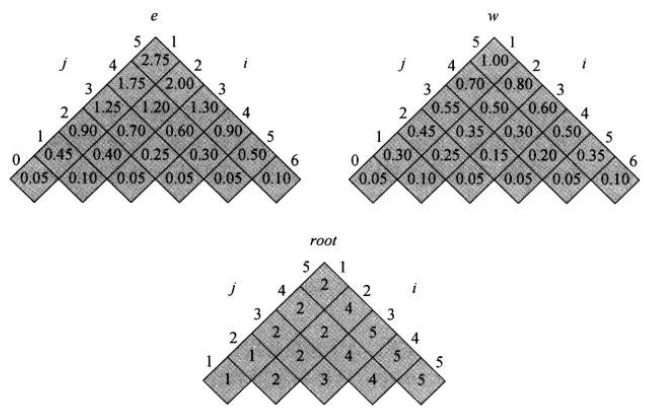
C++实现
1 |
|
已经证明对于所有\(1\le i < j\le n\)，存在最优二叉搜索树，其根满足\(\text{root}[i, j-1] \le \text{root}[i, j] \le \text{root}[i+1, j]\)，根据此使得时间复杂度减小为\(O(n^2)\)
C++实现
1 |
|
参考：算法导论