首先介绍图的表示和图的搜索。图的搜索指的是系统化跟随图中的边来访问图中每个节点
图的表示
对于图\(G=(V, E)\),有两种表示方法:邻接链表和邻接矩阵,两者都可以表示有向图和无向图。邻接链表在表示稀疏图(边数\(|E|\)远远小于\(|V|^2)\)的图)时非常紧凑而称为通常的选择。在稠密图中(边数\(|E|\)接近\(|V|^2)\)的图)倾向于使用邻接矩阵表示法。如果需要快速判断两个节点之间是否有边相连,需要使用邻接矩阵表示法
对于图\(G=(V, E)\),邻接链表表示由一个包含\(|V|\)条链表数组\(Adj\)构成,每个节点有一条链表。\(Adj[u]\)包含图\(G\)中所有与\(u\)邻接的结点(有边相连的节点,也可以说链表里包含指向这些节点的指针)。下图是有向图和无向图两种表示(上面是无向图,下面是有向图)
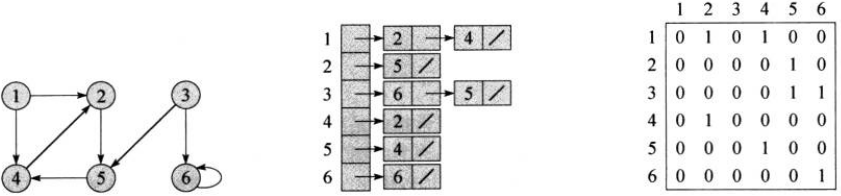 如果图\(G\)是一个有向图,对于边\((u, v)\)来说,节点\(v\)将出现在链表\(Adj[u]\)里面,因此所有的链表长度之和为\(|E|\)。如果图\(G\)是一个无向图,对于边\((u, v)\)来说,节点\(v\)将出现在\(Adj[u]\)和\(Adj[v]\)里面,因此所有邻接链表的长度之和为\(2|E|\),邻接链表表示法的空间均为\(O(V+E)\)
如果图\(G\)是一个有向图,对于边\((u, v)\)来说,节点\(v\)将出现在链表\(Adj[u]\)里面,因此所有的链表长度之和为\(|E|\)。如果图\(G\)是一个无向图,对于边\((u, v)\)来说,节点\(v\)将出现在\(Adj[u]\)和\(Adj[v]\)里面,因此所有邻接链表的长度之和为\(2|E|\),邻接链表表示法的空间均为\(O(V+E)\)
可以直接将边\((u, v))\)的权重值\(\omega\)存放在节点\(u\)的邻接链表里,用来表示权重图。邻接链表的一个缺点是无法快速判断一条边\((u, v)\)是否是图中的一条边,唯一的方法是在邻接链表\(Adj[u]\)里搜索节点\(v\)。邻接矩阵可以克服这个确定,代价是更高的空间复杂度
对于邻接矩阵来说,通常会将图中的节点编号为\(1, 2, \dots, |V|\),则图\(G\)的邻接矩阵由一个\(|V|\times |V|\)矩阵\(A = (a_{ij})\)表示,满足$$a_{ij} = \begin{cases}1 \quad \text{若}(i, j)\in E \\ 0 \quad \text{其他}\end{cases}$$空间复杂度为\(O|V|^2\)
无向图的邻接矩阵是对称矩阵,即\(A = A^T\),在某些应用中可以只存储上三角矩阵(加主对角线),从而减小空间需求。邻接矩阵也可以用来表示权重图,可以直接将边\((u, v)\)的权重\(\omega\)放在第\(u\)行第\(v\)列,对于不存在的边用\(0\)或者\(\infty\)来表示
广度优先搜索
给定图\(G=(V, E)\)和一个可识别的源节点\(s\),广度优先搜索对图\(G\)中的边进行系统性探索来发现可以从源节点\(s\)到达的所有节点。该算法可以计算从源节点\(s\)到达每个可到达的节点距离(最少的边数),同时生成一颗“广度优先搜索树”。该算法需要在发现所有距离源节点\(s\)为\(k\)的所有节点之后,才会发现距离源节点\(k+1\)的其他节点
为了跟踪算法的进展,广度优先搜索在概念上将每个节点涂上白色、灰色或者黑色。所有节点在开始时均涂上白色,随着算法的推进,这些节点可能会变为灰色或者黑色。第一次遇上一个节点,则称该节点被发现,节点颜色会发生变化,因此灰色或者黑色节点表示已经被发现的节点。其中黑色节点表示邻接的节点都已经被发现,灰色节点表示其邻接节点有可能存在未被发现的白色节点。
广度优先搜索伪代码如下,其中节点\(u\)的颜色放在\(u.color\),前驱放在\(u.\pi\),到源节点\(s\)距离放在\(u.d\)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19BFS(G, s)
for each vertex u in {G.V - {s}}
u.color = WHITE
u.d = infty
u.pi = NIL
s.color = GRAY
s.d = 0
s.pi = NIL
Q = empty // 一个队列
ENQUEUE(Q, s);
while Q is not empty
u = DEQUEUE(Q)
for each v in G.Adj[u]
if v.color == WHITE
v.color = GRAY
v.d = u.d + 1
v.pi = u
ENQUEUE(Q, v)
u.color = BLACK
时间复杂度为\(O(V+E)\)。下图是伪代码示意图说明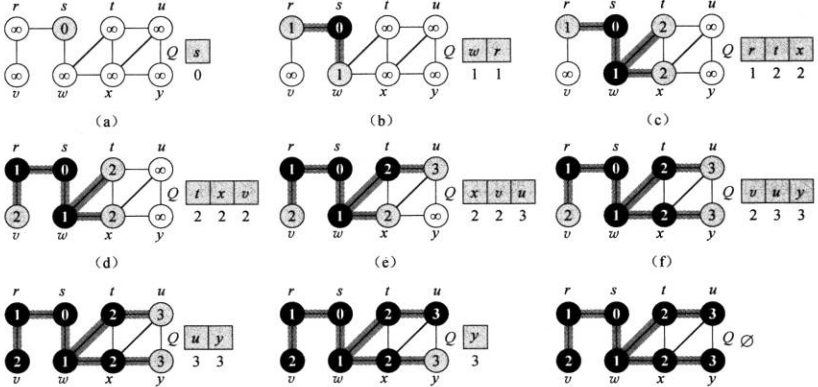 下面的伪代码给出从源节点\(s\)到节点\(v\)的一条最短路径上的所有节点
下面的伪代码给出从源节点\(s\)到节点\(v\)的一条最短路径上的所有节点1
2
3
4
5
6
7PRINT-PATH(G, s, v)
if v == s
print s
else if v.pi == NIL
print "no path form" s "to" v "exists"
else PRINT-PATH(G, s, v.pi)
print v
深度优先搜索
深度优先搜索总是对最近才发现的节点\(v\)的出发边进行探索,直到该节点的所有出发边都被发现为止。一旦节点\(v\)的所有出发边都被发现,搜索则回溯到\(v\)的前驱节点(\(v\)是经过此节点才被发现的),来搜索该前驱节点的所有出发边。该过程一直持续到从源节点可以到达的所有节点都被发现为止,如果还存在尚未被发现的节点,则深度优先搜索将从这些节点中任意选择一个作为新的源节点,重复上述过程
像广度优先搜索一样,深度优先搜索在搜索过程中也是对节点进行涂色来指明节点的状态。每个节点的初始颜色都是白色,在节点被发现后变为灰色,在其邻接链表被扫描完成后变为黑色。该方法保证每个节点仅在一棵深度优先树中出现,因此所有的深度优先树是不相交的
过程中,深度优先搜索还在每个节点上盖一个时间戳。每个节点\(v\)有两个时间戳:第一个时间戳\(v.d\)记录节点\(v\)第一次被发现时间(涂上灰色的时候),第二个时间戳\(v.f\)记录搜索完成对\(v\)的邻接链表扫描的时间(涂上黑色的时候)
下图给出深度优先搜索的伪代码,发现节点\(u\)的时刻记录在属性\(u.d\)中,完成对节点\(u\)处理的时刻记录在属性\(u.f\)中。由于\(|V|\)个节点中每个节点只有发现和完成两个事件,所有这些时间戳范围在\(1-2|V|\),显然对于每个节点\(u\),有$$u.d < u.f$$节点在时刻\(u.d\)之前为白色,在\(u.d\)和\(u.f\)之间为灰色,在时刻\(u.f\)之后为黑色1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20DFS(G)
for each vertex u in G.V
u.color = WHITE
u.pi = NIL
time = 0
for each vertix u in G.V
if u.color == WHITE
DFS-VISIT(G, u)
DFS-VISIT(G, u)
time += 1
u.d = time
u.color = GARY
for each v in G:Adj[u]
if v.color == WHITE
v.pi = u
DFS-VISIT(G, v)
u.color = BLACK
time += 1
u.f = time
时间复杂度为\(O(V+E)\)。下图给出深度优先搜索的过程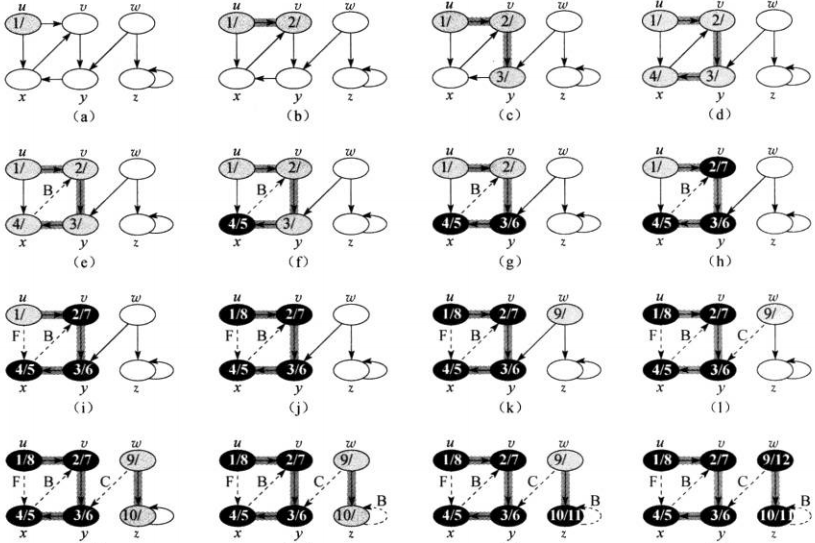
应用实例
Leetcode 1129: Consider a directed graph, with nodes labelled 0, 1, …, n-1. In this graph, each edge is either red or blue, and there could be self-edges or parallel edges. Each [i, j] in red_edges denotes a red directed edge from node i to node j. Similarly, each [i, j] in blue_edges denotes a blue directed edge from node i to node j. Return an array answer of length n, where each answer[X] is the length of the shortest path from node 0 to node X such that the edge colors alternate along the path (or -1 if such a path doesn’t exist).
Example1:
Input: n = 3, red_edges = [[0,1],[1,2]], blue_edges = [] Output: [0,1,-1]
Example 2:
Input: n = 3, red_edges = [[0,1]], blue_edges = [[2,1]] Output: [0,1,-1]
Example 3:
Input: n = 3, red_edges = [[1,0]], blue_edges = [[2,1]] Output: [0,-1,-1]
Example 4:
Input: n = 3, red_edges = [[0,1]], blue_edges = [[1,2]] Output: [0,1,2]
Example 5:
Input: n = 3, red_edges = [[0,1],[0,2]], blue_edges = [[1,0]] Output: [0,1,1]
主要思路:
- 因为每条边有颜色,首先需要构建两个图,分别保存红色边和蓝色边(邻接链表表示法)
- 构建一个结构体,保存当前节点距离节点\(0\)的距离、期待的下一个节点颜色、及当前节点编号(用于访问图表示链表)
- 利用队列结构,根据当前的节点期待的下一个节点颜色,进行入队操作
C++实现(广度优先搜索 BFS)
1 | class Solution { |
参考:算法导论