奇异值分解

奇异值分解(singular value decomposition, SVD)是一种矩阵因子分解方法，任意一个$m\times n$矩阵，都可以表示为三个矩阵的乘积形式（因子分解）。矩阵的奇异值分解一定存在，但不唯一，奇异值分解可以看作矩阵数据压缩的一种方式，即用因子分解近似表示原始矩阵

定义：矩阵的奇异值分解是指将一个非零的$m\times n$实矩阵$A$，$A\in \mathbb{R} ^{m\times n}$，表示为以下三个实矩阵乘积的形式$$A = U\Sigma V^T$$其中$U$是$m$阶正交矩阵，$V$是$n$阶正交矩阵，$\Sigma$ 是由降序排列的非负的对角元素组成的$m\times n$的矩形对角矩阵满足下面等式
$$\begin{equation}\begin{aligned}
& UU^T = I\\
& VV^T = I\\
& \Sigma = \text{diag}(\sigma_1, \sigma_2, \dots, \sigma_p)\\
& p = \text{min}(m, n)\\
& \sigma_1 \ge\sigma_2\ge\dots\ge\sigma_p\ge 0
\end{aligned}\end{equation}$$$U\Sigma V^T$称为矩阵$A$的奇异值分解，$\sigma_i$称为矩阵$A$的奇异值，$U$的列向量称为左奇异向量，$V$的列向量称为右奇异向量
奇异值分解不要求矩阵$A$是方阵

紧奇异值分解与截断奇异值分解

$A = U\Sigma V^T$称为矩阵的完全奇异值分解(full singular value decomposition)，实际中常用的奇异值分解是紧奇异值分解和截断奇异值分解。紧奇异值分解是与原始矩阵等秩的奇异值分解，截断奇异值分解是比原始矩阵低秩的奇异值分解

紧奇异值分解

设有$m\times n$的实矩阵$A$，其秩为$\text{rank}(A)=r, \quad r\le \text{min}(m, n)$，称$U_r\Sigma_r V_r ^T$为矩阵$A$的紧奇异值分解，即$$A = U_r\Sigma_r V_r ^T$$其中$U_r$是$m\times r$的矩阵，$V_r$是$n\times r$的矩阵，$\Sigma_r$是$r$阶对角矩阵。矩阵$U_r$由完全奇异值分解中$U$的前$r$列，$V_r$由$V$的前$r$列，$\Sigma_r$由$\Sigma$的前$r$个对角元素得到。紧奇异值分解对角矩阵$\Sigma_r$的秩与原始矩阵的秩相同

截断奇异值分解

在矩阵的奇异值分解中只取最大的$k$个奇异值（$k < r, r$为矩阵的秩）对应的部分得到截断奇异值分解，实际中奇异值分解通常指截断奇异值分解
设有$m\times n$的实矩阵$A$，其秩为$\text{rank}(A)=r$，且$0 < k < r$，则称$U_k\Sigma_k V_k ^T$为矩阵$A$的截断异值分解(truncated singular value decomposition)，即$$A \approx U_k\Sigma_k V_k ^T$$其中$U_k$是$m\times k$的矩阵，$V_k$是$n\times k$的矩阵，$\Sigma_k$是$k$阶对角矩阵。矩阵$U_k$由完全奇异值分解中$U$的前$k$列，$V_k$由$V$的前$k$列，$\Sigma_k$由$\Sigma$的前$k$个对角元素得到，对角矩阵$\Sigma_k$的秩比原始矩阵的秩低

对矩阵数据进行压缩，奇异值分解提供一种解决方式，紧奇异值分解对应无损压缩，截断奇异值分解对应有损压缩

几何解释

从线性变化的角度理解奇异值分解，$m\times n$矩阵$A$表示从$n$维空间$\mathbb{R}^n$到$m$维空间$\mathbb{R}^m$的一个线性变换，即$$T:x\rightarrow Ax$$其中$x\in \mathbb{R}^n$， $Ax\in \mathbb{R}^m$，$x$和$Ax$分别为各自空间的向量。线性变换可以分解为三个简单的变换：一个坐标系的旋转变换，一个坐标轴的缩放变换，另一个坐标系的旋转变换，根据奇异值分解定理，这种分解变换一定存在
对矩阵$A$进行奇异值分解，得到$A = U\Sigma V^T$，其中$U$和$V$都是正交矩阵，所以$V$的列向量$v_1, v_2, \dots, v_n$构成$\mathbb{R}^n$空间的一组标准正交积，表示$\mathbb{R}^n$空间中的正交坐标系的旋转变换；$U$的列向量$u_1, u_2, \dots, u_m$构成$\mathbb{R}^m$空间的一组标准正交积，表示$\mathbb{R}^m$空间中的正交坐标系的旋转变换；$\Sigma $的对角元素$\sigma_1, \sigma_2, \dots, \sigma_n$是一组非负实数，表示$\mathbb{R}^n$中的原始正交坐标系坐标轴的$\sigma_1, \sigma_2, \dots, \sigma_n$倍的缩放变换
任意一个向量$x\in \mathbb{R}^n$，经过基于$A = U\Sigma V^T$的线性变换，等价于经过坐标系的旋转变换$V^T$，坐标轴的缩放变换$\Sigma$及坐标系的旋转变换$U$得到向量$Ax\in \mathbb{R}$。下图直观给出几何解释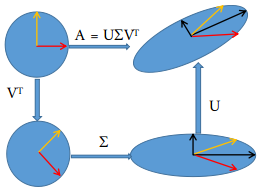奇异值分解几何解释

SVD的主要性质

设矩阵$A$的奇异值分解为$A=U\Sigma V^T$，则以下关系成立$$\begin{equation}\begin{aligned}& A^T A = (U\Sigma V^T)^T(U\Sigma V^T) = V(\Sigma ^T \Sigma)V^T\\& AA^T = (U\Sigma V^T)(U\Sigma V^T)^T = U(\Sigma \Sigma ^T)U^T\end{aligned}\end{equation}$$可知矩阵$AA^T$和$A^T A$的特征分解存在，可由矩阵$A$的奇异值分解表示。$V$的列向量是$A^T A$的特征向量，$U$的列向量是$AA^T$的特征向量，$\Sigma $的奇异值是$A^T A$和$AA^T$的特征值平方根
在矩阵$A$的奇异值分解中，奇异值，左奇异向量，右奇异向量之间存在对应关系

由$A=U\Sigma V^T$可知$AV=U\Sigma$，观测等式两端的第$j$列可得到$$Av_j = \sigma_j u_j, \quad j = 1, 2, \dots, n$$类似有$A^T U = V\Sigma ^T$，可得到$$A^T u_j = \sigma_j v_j, \quad j = 1, 2, \dots, n \\ A^T u_j = 0, \quad j = n+1, \dots, m$$
矩阵$A$的奇异值分解中，奇异值$\sigma_1, \sigma_2, \dots, \sigma_n$是唯一的，而矩阵$U$和$V$是不唯一的
矩阵$A$和$\Sigma$秩相等，等于正奇异值$\sigma_i$的个数（包含重复的奇异值）

SVD 算法

给定$m\times n$矩阵$A$，按照以下步骤求解矩阵奇异值分解

首先求$A^T A$的特征值和特征向量

计算对称矩阵$W=A^TA$，并求特征方程$$(W-\lambda I)x = 0$$得到特征值$\lambda_i (i=1, 2, \dots, n)$，将特征值由大到小排列$$\lambda_1\ge\lambda_2\ge\dots\ge\lambda_n\ge 0$$并带入求对应的特征向量
求$n$阶正交矩阵$V$

将得到的特征向量单位化，得到单位特征向量$v_1, v_2, \dots, v_n$，构成$n$阶正交矩阵$V$$$V = \big[v_1, v_2, \dots, v_n\big]$$
求$m\times n$对角矩阵$\Sigma$

计算矩阵$A$的奇异值$$\sigma_i = \sqrt{\lambda_i}, \quad i = 1, 2, \dots, n$$构造$m\times n$矩形对角矩阵$Sigma$，主对角线元素是奇异值，其余元素为$0$$$\Sigma = \text{diag}(\sigma_1, \sigma_2, \dots, \sigma_n)$$
求$m$阶正交矩阵$U$

对矩阵$A$的前$r$个正奇异值（也就是所有的正奇异值），根据$Av_j = \sigma_j u_j, \quad j = 1, 2, \dots, n$令$$u_j = \dfrac{1}{\sigma_j}Av_j, \quad j = 1, 2, \dots, r$$可得到$$U_1 = \big[u_1, u_2, \dots, u_r\big]$$求$A^T$的零空间（即$A^Tx=0$的解构成的空间）的一组标准正交基${u_{r+1}, u_{r+2}, \dots, u_m}$令$$U_2 = \big[u_{r+1}, u_{r+2}, \dots, u_m\big]$$令$U = [U_1, U_2]$
得到奇异值分解$$A = U\Sigma V^T$$

应用

奇异值分解可以被用来计算矩阵的广义逆阵（伪逆）。若矩阵$M$的奇异值分解为$M = U\Sigma V^T$那么$M$的伪逆为$$M^+ = V \Sigma^+ U^T$$其中$\Sigma^+$是$\Sigma$的伪逆，是将$\Sigma$主对角线上每个非零元素都求倒数之后再转置得到的。求伪逆通常可以用来求解最小二乘法问题。
奇异值分解在统计中的主要应用为主成分分析（PCA）。数据集的特征值（在SVD中用奇异值表征）按照重要性排列，降维的过程就是舍弃不重要的特征向量的过程，而剩下的特征向量张成空间为降维后的空间。
矩阵数据压缩

参考：统计学习方法（第二版）–李航