主成分分析(PCA)

常用的无监督学习方法，利用正交变换将线性相关变量表示的观测数据转换为少数几个线性无关变量表示的数据，功能有降维和去相关性

引言

主成分分析中，首先对给定数据进行规范化，使得数据各个变量均值为$0$，方差为$1$，之后对数据进行正交变换（理解为旋转），将原来由线性相关变量表示数据变为若干个线性无关新变量表示的数据。新变量是可能的正交变换中变量方差和最大的（在信号处理中认为信号具有较大的方差，噪声有较小的方差），将新变量依次称为第一主成分，第二主成分等等。
主成分分析直观理解：样本中的数据可以用空间中的一个点表示（正交坐标系，每一个轴表示一个变量/特征），规范化处理后，样本数据分布在原点附近。对原坐标系进行主成分分析等价于进行坐标旋转变换，将数据投影到新的坐标轴上。新坐标系第一坐标轴，第二坐标轴分别表示第一主成分，第二主成分等，数据在每一个坐标轴上的平方表示相应变量的方差，且新的坐标系在所有可能的坐标系中，坐标轴上的方差和最大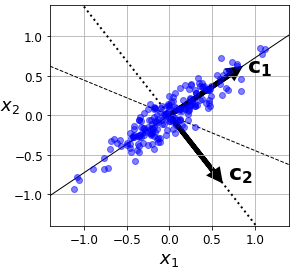 主成分分析示例图中，数据由$x_1$和$x_2$表示，数据已经规范化处理，数据以原点为中心分布在倾斜的椭圆中，图中可知$x_1$和$x_2$是线性相关的（当知道其中一个变量$x_1$的取值时对另一个变量$x_2$的预测不是完全随机的）。主成分分析对数据进行正交变换，即对原坐标系进行旋转变换，将数据在新坐标系表示。数据在原坐标系的表示由$x_1$和$x_2$变为在新坐标系的$c_1$和$c_2$，主成分分析选择方差最大的方向（第一主成分）作为新坐标系的第一坐标轴，图中对应椭圆的长轴，之后选择与第一坐标轴正交，且方差次之的方向，图中对应的椭圆短轴作为新坐标系的第二坐标轴。在新坐标系中变量$c_1$和$c_2$是线性无关的。
方差最大等价于主成分分析在旋转变换中选取离样本点距离平方和最小的轴作为主成分
在数据总体上进行的主成分分析称为总体主成分分析，在有限样本数据上进行的主成分分析称为样本主成分分析（实际中的情况）

总体主成分分析

定理：设$\boldsymbol x$是$m$维随机变量，即$\boldsymbol x = (x_1, x_2, \dots, x_m)^T$，$\Sigma$是$\boldsymbol x$的协方差矩阵，$\Sigma$的特征值分别为$\lambda_1\ge\lambda_2\ge\dots\ge\lambda_m\ge 0$，特征值对应的单位特征向量分别为$\alpha_1, \alpha_2, \dots, \alpha_m$，则$\boldsymbol x$的第$k$个主成分为$$y_k=\alpha_k ^T \alpha = \alpha_{1k} x_1 + \alpha_{2k} x_2 + \dots + \alpha_{mk} x_m, k=1, 2, \dots, m$$$\boldsymbol x$的第$k$主成分的方差为$$\text{var}(y_k)=\alpha_k ^T \Sigma \alpha_k = \lambda_k, k = 1, 2, \dots, m$$
证明: 求第一主成分$y_1 = \alpha_1 ^T\boldsymbol x$的系数$\alpha_1$，根据主成分的定义，$\alpha_1$是在$\alpha_1 ^T\alpha_1 = 1$的条件下，$\boldsymbol x$的所有变换中使得方差$$\text{var}(\alpha_1 ^T \boldsymbol x) = \alpha_1 ^T \Sigma \alpha_1$$最大的系数$\alpha_1$。也即求下面的约束条件$$\begin{equation}\begin{aligned}\underbrace{\max}_{\alpha_1}\qquad \alpha_1 ^T \Sigma \alpha_1 \\ s.t. \qquad \alpha_1 ^T \alpha_1 = 1\end{aligned}\end{equation}$$定义拉格朗日函数$$
\alpha_1 ^T \Sigma \alpha_1 - \lambda (\alpha_1 ^T \alpha_1 - 1)$$对$\alpha_1$其求导得到$$\Sigma \alpha_1 - \lambda \alpha_1 = 0$$即$\lambda $是$\Sigma $的特征值，$\alpha_1$是对应的单位特征向量。
求第二主成分$y_2 = \alpha_2 ^T\boldsymbol x$的系数$\alpha_2$，根据主成分的定义，$\alpha_2$是在$\alpha_2 ^T\alpha_2 = 1$且$\alpha_2 ^T \boldsymbol x$与 $\alpha_1 ^T \boldsymbol x $不相关的条件下使得方差$$\text{var}(\alpha_2 ^T \boldsymbol x) = \alpha_2 ^T \Sigma \alpha_2$$最大的系数$\alpha_2$。也即求下面的约束条件$$\begin{equation}\begin{aligned}\underbrace{\max}_{\alpha_2}\qquad \alpha_2 ^T \Sigma \alpha_2 \\ s.t. \qquad \alpha_1 ^T \Sigma \alpha_2 &= 0, \quad\alpha_2 ^T \Sigma \alpha_1 = 0\\\qquad \alpha_2 ^T\alpha_2 &= 1\end{aligned}\end{equation}$$注意到$$\alpha_1 ^T \Sigma \alpha_2 =\alpha_2 ^T \Sigma \alpha_1 = \alpha_2 ^T \lambda_1 \alpha_1 = \lambda_1 \alpha_2 ^T \alpha_1 = \lambda_1 \alpha_1 ^T \alpha_2$$其中$\alpha_2 ^T \alpha_1$是标量，所以有$(\alpha_2 ^T \alpha_1)^T = \alpha_2 ^T \alpha_1$。以及根据主成分定义有$\alpha_2 ^T \alpha_1 = \alpha_1 ^T \alpha_2 = 0$（$\alpha_i$是正交的），可定义拉格朗日函数$$\alpha_2 ^T \Sigma \alpha_2 - \lambda(\alpha_2 ^T \alpha_2 - 1) - \phi \alpha_2 ^T \alpha_1$$对$\alpha_2$求导并令其为$0$得到$$2\Sigma \alpha_2 - 2\lambda \alpha_2 - \phi \alpha_1 = 0$$对上式左乘$\alpha_1 ^T$有$$2\alpha_1 ^T \Sigma \alpha_2 - 2\lambda \alpha_1 ^T \alpha_2 - \phi \alpha_1 ^T \alpha_1 = 0$$可知前两项为$0$，且$\alpha_1 ^T \alpha_1 = 1$因此有$\phi = 0$，带入拉格朗日求导等式中得到$$\Sigma \alpha_2 - \lambda \alpha_2 = 0$$即$\lambda $是$\Sigma $的特征值，$\alpha_2$是对应的单位特征向量，同理对于其他的主成分也有类似的结论
推论：$m$维随机变量，即$\boldsymbol y = (y_1, y_2, \dots, y_m)^T$的分量依次是$\boldsymbol x$的第一主成分到第$m$主成分的充要条件是：

$\boldsymbol y = A^T \boldsymbol x$，$A$是正交矩阵$$
\begin{bmatrix}
\alpha_{11} & \alpha_{12} & \dots & \alpha_{1m} \\
\alpha_{21} & \alpha_{22} & \dots & \alpha_{2m} \\
\vdots & \vdots & & \vdots \\
\alpha_{m1} & \alpha_{m2} & \dots & \alpha_{mm} \\
\end{bmatrix}$$

$\boldsymbol y$的协方差矩阵为对角矩阵$$\text{cov}(\boldsymbol y) = \text{diag}(\lambda_1, \lambda_2, \dots, \lambda_m) \\ \lambda_1\ge\lambda_2\ge\dots\ge\lambda_m$$其中$\lambda_k$是$\Sigma$（$\boldsymbol x$的协方差矩阵）第$k$个特征值，$\alpha_k$是对应的单位特征向量

根据之前证明可知，有$\Sigma \alpha_k = \lambda_k \alpha_k $ 写成矩阵的形式为$$\Sigma A = A\Lambda$$其中$\Lambda$是对角矩阵（即$\boldsymbol y$的协方差矩阵），因为$A$是正交矩阵，有$A^T A = AA^T = I$，可得到$A^T\Sigma A = A^T A\Lambda = \Lambda$和$\Sigma = A\Lambda A^T$
总体主成分$\boldsymbol y$的方差之和等于随机变量$\boldsymbol x$的方差之和，即$\sum_{i=1}^{m}\lambda_i = \sum_{i=1}^{m}\sigma_{ii}$其中$\sigma_{ii}$是$\boldsymbol x$的协方差矩阵$\Sigma$的对角元素（证明就不写了，比较简单，利用上一段讨论的结论）

主成分的个数

PCA的主要目的是降维，所以一般选择$k$($k \ll m$)（线性无关）代替原来的$m$（线性相关）个变量，同时保留原有变量的大部分信息（信息指原有变量的方差），给出两个定义

第$k$个主成分$y_k$的方差贡献率定义为$y_k$的方差与所有方差之和的比，即$$\eta_k = \dfrac{\lambda_k}{\sum_{i=1}^{m}\lambda_i}$$
$k$个主成分$y_1, y_2, \dots, y_k$累积方差贡献率定义为$k$个方差之和与所有方差之和的比值，即$$\sum_{i=1}^{k}\eta_i = \dfrac{\sum_{i=1}^{k}\lambda_i}{\sum_{i=1}^{m}\lambda_i}$$

通常取$k$使得累积方差贡献率达到规定百分比以上，例如$70\%\sim 80\%$以上，累积方差贡献率反映主成分保留信息比例。

规范化变量

在实际问题中，不同变量可能有不同的量纲，直接求主成分有时产生不合理的结果，为了消除这个影响，通常对各个随机变量实施标准化，使其均值为$0$，方差为$1$，即$$x_i ^* = \dfrac{x_i - E(x_i)}{\sqrt{\text{var}(x_i)}}$$

样本主成分分析

实际问题中，需要在观测数据上进行主成分分析，也就是在样本上进行主成分分析

假设对$m$维随机变量$\boldsymbol x = (x_1, x_2, \dots, x_m)^T$进行$n$次的独立观测，$\boldsymbol x_1, \boldsymbol x_2, \dots, \boldsymbol x_n$表示观测样本，其中$\boldsymbol x_j = (x_{1j}, x_{2j}, \dots, x_{mj})^T$表示第$j$个观测样本，观测数据用样本矩阵$\boldsymbol X$表示为$$\boldsymbol X = [\boldsymbol x_1, \boldsymbol x_2, \dots, \boldsymbol x_n]=
\begin{bmatrix}
x_{11} & x_{12} & \dots & x_{1n}\\
x_{21} & x_{22} & \dots & x_{2n}\\
\vdots & \vdots & & \vdots \\
x_{m1} & x_{m2} & \dots & x_{mn}
\end{bmatrix}$$给定样本矩阵$\boldsymbol X$，可以估计样本均值$\bar{x}$及样本协方差矩阵$S$
$$\begin{equation}\begin{aligned}\bar{x} &= \dfrac{1}{n}\sum_{j=1}^{n}\boldsymbol x_j \\
S &= [s_{ij}]_{m\times m} \\
s_{ij} &= \dfrac{1}{n-1}\sum_{k=1}^{n}(x_{ik}-\bar{x_i})(x_{jk}-\bar{x_j}),\quad i, j = 1, 2, \dots, m
\end{aligned}\end{equation}$$其中$\bar{x_i} = \dfrac{1}{n}\sum_{k=1}^{n}x_{ik}$ 是第$i$个变量样本均值，$\bar{x_j} = \dfrac{1}{n}\sum_{k=1}^{n}x_{jk}$ 是第$j$个变量样本均值。
样本矩阵的相关矩阵$R$（也叫相关系数矩阵，由矩阵各行的相关系数组成）$$R = [r_{ij}]_{m\times m}, \quad r_{ij}=\dfrac{s_{ij}}{\sqrt{s_{ii}s_{jj}}}, \quad i, j = 1, 2, \dots, m$$

数据矩阵奇异值分解算法

PCA在过程中要计算协方差矩阵，当样本数和特征数很多的时候，这个计算量是相当大的，给定样本矩阵$\boldsymbol X$，利用数据矩阵奇异值分解进行主成分分析

假设有$k$个主成分，对于$m\times n$的实矩阵$A$，假设其秩为$r$，有$0 < k < r$，可将矩阵$A$进行截断奇异值分解$$A\approx U_k\Sigma_k V_k ^T$$其中$U_k$是$m\times n$矩阵，$V_k$是$n\times k$矩阵，$\Sigma_k$是$k$阶对角矩阵，$U_k$，$V_k$分别取矩阵$A$的完全奇异值分解矩阵$U$，$V$的前$k$列，$\Sigma_k$由矩阵$A$的完全奇异值分解矩阵$\Sigma$的前$k$个对角元素
定义一个新的矩阵$\boldsymbol {X’}$$$\boldsymbol {X’}=\dfrac{1}{\sqrt{n-1}}\boldsymbol {X^T}$$其中$\boldsymbol {X’}$的每一列均值为$0$，可得到$$\begin{equation}\begin{aligned}\boldsymbol {X’ ^T}\boldsymbol {X’} &= \Bigg(\dfrac{1}{\sqrt{n-1}}X^T\Bigg)^T\Bigg(\dfrac{1}{\sqrt{n-1}}X^T\Bigg)\\ &= \dfrac{1}{\sqrt{n-1}}XX^T\end{aligned}\end{equation}$$即$\boldsymbol {X’ ^T}\boldsymbol {X’}$等于样本矩阵$\boldsymbol X$的协方差矩阵$S_X$，$S_X = \boldsymbol {X’ ^T}\boldsymbol {X’}$
根据之前讨论，主成分分析是求协方差矩阵$S_X$的特征值和对应的单位特征向量，因此问题转化为求矩阵$\boldsymbol {X’ ^T}\boldsymbol {X’}$的特征值和对应的单位特征向量
假设$\boldsymbol {X’}$的截断奇异值分解为$\boldsymbol {X’} = U\Sigma V^T$，则$V$的列向量就是$S_X = \boldsymbol {X’ ^T}\boldsymbol {X’}$的单位特征向量。因此求$\boldsymbol X$的主成分可以通过求$\boldsymbol {X’}$的奇异值来实现

证明：$$S_X = \boldsymbol {X’ ^T}\boldsymbol {X’} = (U\Sigma V^T)^T(U\Sigma V^T)=V\Sigma ^2 V^T$$由于$VV^T = I$，上式满足特征值分解公式，所以$V$的列向量是$S_X$的单位特征向量

算法
输入：$m\times n$样本矩阵$\boldsymbol X$，其中每一行元素的均值为$0$
输出：$k\times n$的样本主成分矩阵$\boldsymbol Y$
参数：主成分的个数$k$

构造新的$n\times m$矩阵$$\boldsymbol {X’}=\dfrac{1}{\sqrt{n-1}}\boldsymbol X ^T$$其中$\boldsymbol {X’}$的每一列的均值为$0$
对矩阵$\boldsymbol {X’}$进行截断奇异值分解，得到$$\boldsymbol {X’} = U\Sigma V^T$$有$k$个奇异值、奇异向量。矩阵$V$的前$k$列构成$k$个样本主成分
求$k\times n$样本主成分矩阵$$\boldsymbol Y = V^T \boldsymbol X$$

参考：统计学习方法（第二版）–李航

浅谈机器学习中主成分分析-PCA