模型训练
线性模型
解析解
直接使用解析解(closed-form)计算模型参数
线性回归模型如下$$\hat{y}=h_{\theta}(\mathbf{x}) = \theta ^T\mathbf{x}$$其中\(\theta = [\theta_0, \theta_1, \dots, \theta_n]^T\),\(\mathbf{x}=[1, x_1, x_2, \dots, x_n]^T\)
训练一个模型意味着学习模型参数,使其尽可能拟合训练数据。因此需要寻找一种度量手段(损失函数),用来度量模型拟合数据的程度。对于线性回归模型,选择平方误差损失(MSE),其表达式如下$$\text{MSE}(\mathbf{X}, h_{\theta})=\dfrac{1}{m}\sum_{i=1}^{m}(\theta ^T \mathbf{x}^{(i)}-y^{(i)})^2$$对参数\(\theta\)求导,得到$$\hat{\theta}=(\mathbf{X^T}{\mathbf{X}})^{-1}\mathbf{X}^T\mathbf{y}$$其中\(\mathbf{X} \in (m\times n)\),\(m\)是样本个数,\(n\)是特征个数
python实现
1 | import numpy as np |
缺点:对于大规模特征或者样本,解析解在实际中并不实用
迭代优化
使用迭代的优化方法,例如梯度下降(GD),实际使用中有Batch GD、Mini-batch GD和Stochastic GD
梯度下降的一般思路是通过迭代微调参数,使得损失函数最小化。沿着梯度最大的方向下降:计算损失函数对模型参数的局部梯度,然后沿着其梯度方向下降,一旦梯度为\(0\),则优化停止(开始时,模型参数需要随机初始化)学习率(步长)是一个重要的超参数,如果太小,算法收敛慢,如果太大,算法可能不收敛
损失函数非凸,不能保证找到全局最优解。MSE损失函数为凸函数,可以保证找到全局最优解,事实上MSE的损失函数像一个碗,如下图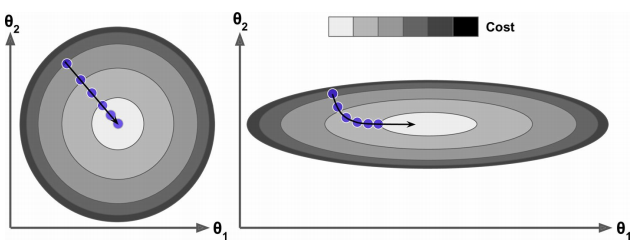 左边特征\(1\)和特征\(2\)有相同的尺度,右边特征\(1\)的尺度比特征\(2\)的尺度小。左边梯度下降算法直接朝向损失函数最小值方向,可以较快收敛,右边首先沿着和全局最小值几乎正交的方向,然后在较平的部分花费许多步,最终会达到最小值,但花费更多时间。当使用梯度下降时候,应该保证所有的特征有相似的尺度
左边特征\(1\)和特征\(2\)有相同的尺度,右边特征\(1\)的尺度比特征\(2\)的尺度小。左边梯度下降算法直接朝向损失函数最小值方向,可以较快收敛,右边首先沿着和全局最小值几乎正交的方向,然后在较平的部分花费许多步,最终会达到最小值,但花费更多时间。当使用梯度下降时候,应该保证所有的特征有相似的尺度
批梯度下降(Batch Gradient Descent)
应用梯度下降法,需要计算损失函数对每一个参数\(\theta_j\)的梯度,然后更新每一个参数。下面是计算损失函数对参数\(j\)的梯度$$\dfrac{\partial}{\partial\theta_j}\text{MSE}(\theta) = \dfrac{2}{m}\sum_{i=1}^{m}(\theta ^T\mathbf{x^{(i)}}-y^{(i)})x_j ^{(i)}$$实际中常计算梯度向量$$
\bigtriangledown _{\theta}\text{MSE}(\theta) =
\begin{bmatrix}
\dfrac{\partial}{\partial \theta_0}\text{MSE}(\theta)\\
\dfrac{\partial}{\partial \theta_1}\text{MSE}(\theta)\\
\vdots \\
\dfrac{\partial}{\partial \theta_n}\text{MSE}(\theta)
\end{bmatrix} = \dfrac{2}{m}\mathbf{X}^T(\mathbf{X}\theta-\mathbf{y})$$其中\(\mathbf{X} \in (m\times n)\),\(m\)是样本个数,\(n\)是特征个数。此公式在每次梯度下降都使用整个训练数据,对于大规模数据,此算法较慢
每一步梯度更新公式如下$$\theta ^{(\text{next}, \text{step})} = \theta - \eta \bigtriangledown _{\theta}\text{MSE}(\theta)$$对于学习率选择可以使用网格搜索。对于迭代次数,可以先设置一个较大的值,当梯度的改变小于阈值\(\varepsilon\)的时候终止算法
杂谈:当损失函数是凸函数,且其梯度比较平滑,则具有固定学习率的Batch Gradient Descent的收敛率为\(O(\dfrac{1}{\text{iterations}})\),也就是说,如果将阈值\(\varepsilon\)缩小10倍(有更高的精度),算法需要运行大约\(10\)倍多次数
python实现
1 | import numpy as np |
随机梯度下降(Stochastic Gradient Descent)
Batch Gradient Descent的缺点是在每次迭代,使用整个训练集去计算梯度,对于大规模训练数据,使得训练的速度较慢。而随机梯度下降(Stochastic Gradient Descent)在每次迭代只选择一个随机样本计算梯度,适合大规模训练数据。
在另一方面,由于选取样本的随机性,SGD对比BGD有较大的波动性,也就是损失函数在平均意义下是下降的,过程是波动的,如下图所示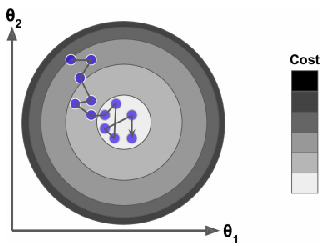 当损失函数下降到最小值时,还是存在波动。当损失函数是非凸时,SGD这种波动性可以帮助算法跳出局部极值,因此和BSD对比,SGD有更好的机会找到全局最小值
当损失函数下降到最小值时,还是存在波动。当损失函数是非凸时,SGD这种波动性可以帮助算法跳出局部极值,因此和BSD对比,SGD有更好的机会找到全局最小值
这种随机性的优点是可以逃出局部最小值,缺点是算法不会稳定在最小值处(波动)。常用的解决方法是,逐渐减小学习率(也称为模拟退火法)。决定在每次迭代的学习率的函数称为学习率表(learning schedule)
python实现
1 | import numpy as np |
上述程序中每一个样本会被随机选择,有些样本可能被选择多次,有些样本可能不会被选择。如果想确保每一个样本都会被选择,可以在每个epoch先打乱训练集(shuffle the training set),然后依次选择样本
Mini-batch 梯度下降
在每一步计算梯度时,随机选择训练集的随机子集(mini-batches)用来计算梯度。mini-batch GD和SGD对比的一个优势是通过矩阵操作,可以得到性能上的提升。下图是mini-batch GD、SGD和BGD训练过程比较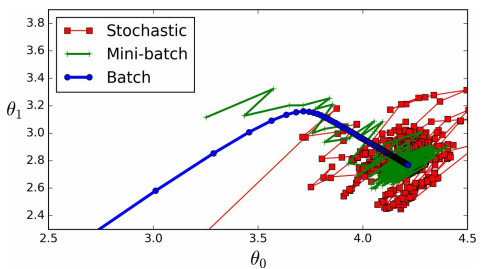 下面的表总结了不同的训练方法比较结果
下面的表总结了不同的训练方法比较结果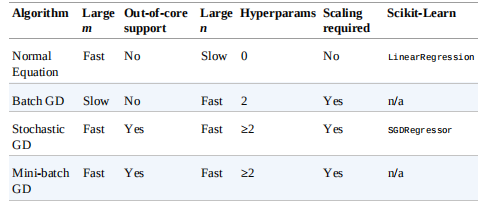 其中\(m\)表示样本的个数,\(n\)表示特征的个数
其中\(m\)表示样本的个数,\(n\)表示特征的个数
模型评估
学习曲线
判断一个模型是过拟合还是欠拟合的一个方法是使用交叉验证:如果模型在训练集上表现好,但根据交叉验证表现差,则模型过拟合;如果模型在两者上都表现差,则模型欠拟合
另一个方法是看学习曲线:即将模型在训练集和验证集上的性能绘图(横轴表示训练集大小,纵轴表示误差),如下图所示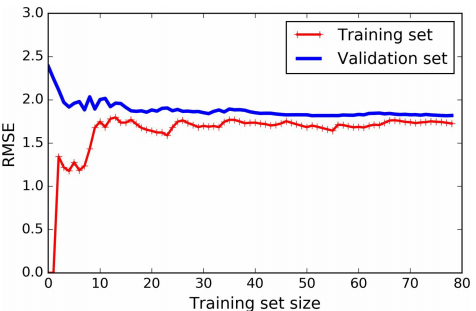 对于训练集的性能,开始时只有一个或者两个样本,模型可以完美拟合,因此训练误差从\(0\)开始;随着训练样本的增多,模型不能很好拟合训练集,即因为数据是有噪声的,也因为数据是非线性的(此模型是线性模型),因此训练误差增加,直到稳定。对于验证集误差,开始时,模型只在很少的训练集上训练,模型的泛化能力差,因此验证集的误差大,随着训练数据的增加,模型的泛化能力增加,验证集误差下降,直到稳定。图中模型欠拟合,因为两者最终的误差都很大
对于训练集的性能,开始时只有一个或者两个样本,模型可以完美拟合,因此训练误差从\(0\)开始;随着训练样本的增多,模型不能很好拟合训练集,即因为数据是有噪声的,也因为数据是非线性的(此模型是线性模型),因此训练误差增加,直到稳定。对于验证集误差,开始时,模型只在很少的训练集上训练,模型的泛化能力差,因此验证集的误差大,随着训练数据的增加,模型的泛化能力增加,验证集误差下降,直到稳定。图中模型欠拟合,因为两者最终的误差都很大
当模型欠拟合时候,增加训练样本并没有作用,需要使用一个更加复杂的模型或者选择更好的特征;当模型过拟合时候,可以增加训练样本,或者限制模型复杂度
偏差方差权衡
模型的泛化错误可以分解为\(3\)部分之和:偏差(bias)、方差(variance)、残差(irreducible error)
- 偏差:由于错误的假设,例如假设数据是线性的,实际上是非线性的。高的偏差模型很可能对训练数据欠拟合
- 方差:由于模型对训练数据中小的变换的过度敏感,一个复杂的模型很可能有高的方差,导致过拟合
- 残差:由于数据本身具有的噪声,减少此误差的唯一方式是清洗数据,例如移除异常值,修复坏的数据源等
模型偏差方差示意图如下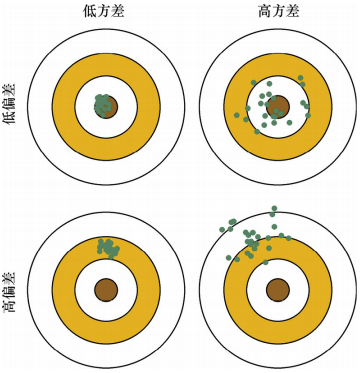
模型正则化
以线性模型为例,通过约束模型的权重来起到正则化的作用,有Ridge Regression、Lasso Regression和Elastic Net。正则化应该只在训练过程中
Ridge Regression
其损失函数如下$$J(\theta) = \text{MSE}(\theta) + \alpha \dfrac{1}{2}\sum_{i=1}^{n}\theta_{i} ^2$$偏置项\(\theta_0\)不需要正则化
Ridge Regression 对输入特征的尺度比较敏感,因此需要对输入数据进行标准化处理,对于大多数正则化模型都应该做标准化处理
其解析解如下$$\hat{\theta} = (\mathbf{X}^T \mathbf{X} + \alpha \mathbf{A})^{-1}\mathbf{X}^T\mathbf{y}$$其中\(\mathbf{A}\)是\(n\times n\)的单位阵(除了左上角的一个元素为\(0\))。实际中一般使用梯度下降训练模型
Lasso Regression
其损失函数如下$$J(\theta) = \text{MSE}(\theta) + \alpha \sum_{i=1}^{n}|\theta_{i}|$$Lasso Regression 回归的一个重要特点是完全消除不重要特征的权重(将其权重设置为\(0\)),自动执行特征选择输出一个稀疏模型
建议:为了逐渐收敛到全局最小值,需要逐渐减小学习率
由于Lasso cost 函数在\(\theta_i = 0\)不可导,当\(\theta_i = 0\),使用一个subgradient vector$$g(\theta,J) = \bigtriangledown _{\theta}\text{MSE}(\theta) + \alpha\begin{bmatrix}\text{sign}(\theta_1) \\
\text{sign}(\theta_2) \\
\vdots \\
\text{sign}(\theta_n) \\
\end{bmatrix} \quad \text{where sign}(\theta_i) = \begin{cases}-1 \quad \text{if} \quad \theta_i < 0 \\
0 \quad \text{if} \quad \theta_i = 0 \\
+1 \quad \text{if} \quad \theta_i > 0
\end{cases}$$
Elastic Net
其损失函数如下$$J(\theta) = \text{MSE}(\theta) + \gamma\alpha\sum_{i=1}^{n}|\theta_i| + \dfrac{1-\gamma}{2}\alpha\sum_{i=1}^{n}\theta_i ^2$$其中\(\gamma\)是Lasso回归和Ridge回归的权衡参数
一般来说,Ridge回归是默认的选择,但当猜想只有几个特征是重要的时候,应该使用Lasso回归或Elastic Net(通常来说,最好使用Elastic Net,因为当特征数目比训练样本多或者有些特征是有相关关系)
Early Stopping
当验证集误差达到最小时(之后模型会过拟合训练数据),停止训练,如下图所示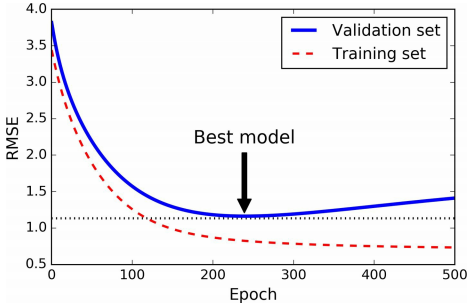
损失函数
对于二分类问题\(Y = {1, -1}\),希望\(\text{sign}f(x_i, \theta) = y_i\),最自然的损失函数是\(0-1\)损失,即$$L_{0-1}(f, y) = \begin{cases}1, \quad 误分类\\ 0, \quad 正确分类\end{cases}$$但是该损失非凸,非光滑,很难优化。实际中常用的损失函数有如下
Hinge损失
$$L_{\text{hinge}}(f, y) = \text{max}\{0, 1-fy\}$$Hinge损失是\(0-1\)损失的凸上界,当\(fy\ge 1\)时,不做任何惩罚。但其在\(fy=1\)处不可导,需要使用次梯度下降法(Subgradient Descent)
Logistic损失
$$L_{\text{logistic}}(f, y) = \log_2(1+e^{-fy})$$Logistic损失是\(0-1\)损失的凸上界,且该函数处处平滑,可以使用梯度下降法进行优化。但是该损失对所有样本点进行惩罚,因此对异常值相对敏感些。
交叉熵损失
当预测值\(f\in[-1, 1]\)时,可以使用交叉熵损失$$L_{\text{cross entropy}}(f, y) = -\log_2\Big(\dfrac{1+fy}{2}\Big)$$交叉熵损失也是\(0-1\)凸上界。四种损失函数曲线如下图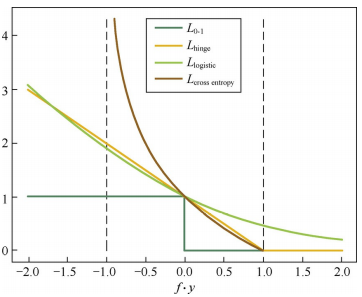 对于回归问题,希望\(f(x_i, \theta)\approx y_i\),常用的损失函数如下
对于回归问题,希望\(f(x_i, \theta)\approx y_i\),常用的损失函数如下
平方损失
$$L_{\text{square}}(f, y) = (f-y)^2$$平方损失函数是光滑的,对异常值敏感(预测值距离真实值远时,惩罚力度大)
绝对损失
$$L_{\text{absolute}}(f, y) = |f-y|$$绝对损失相当于做中值回归,相比做均值回归的平方损失函数,绝对损失函数鲁棒性更强。缺点是在\(f=y\)处不可导
中值(中位数)回归:我们优化的目标是使目标值趋于样本点值的中位数,直观理解就是大于 与 小于 目标值的样本点数尽量相等
均值回归:使目标值趋于样本点值的均值
解释
Huber损失
综合可导性和鲁棒性,可采用Huber损失$$L_{\text{Huber}}(f, y) = \begin{cases}(f-y)^2, \quad |f-y|\le\delta\\2\delta|f-y|-\delta ^2, \quad |f-y| > \delta\end{cases}$$Huber损失在\(|f-y|\)较小时为平方损失,在\(|f-y|\)较大时为线性损失,可导鲁棒。三种损失函数曲线如下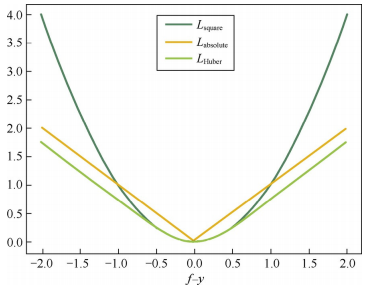
参考:Hands-On Machine Learning with Scikit-Learning & TensorFlow
百面机器学习