决策树
决策树(decision tree)是一种基本的分类与回归方法。主要优点是模型具有可读性、分类速度快。决策树学习包括三个步骤：特征选择、决策树生成、决策树修剪
分类决策树模型是一种描述对实例进行分类的树形结构，决策树由节点和有向边组成。节点有两种类型：内部节点和叶节点，内部节点表示一个特征或者属性、外部节点表示一个类
用决策树分类从根节点开始，对实例的某一特征进行分类，根据测试结果将实例分配到子节点，如此递归对测试实例进行分配，直到到达叶节点，将实例分配到叶节点的类中
决策树学习
决策树学习的本质是从训练数据集中归纳出一组分类规则。与训练数据集不矛盾的决策树（对训练数据集能正确分类）可能有多个，也可能一个都没有，需要找一个与训练数据集矛盾较小的决策树，同时具有很好的泛化能力。如果特征数量较多，可以在决策树学习开始的时候，对特征进行选择，保留对训练数据有足够分类能力的特征
决策树的生成对应模型的局部选择，决策树的剪枝对应模型的全局选择，决策树的生成只考虑局部最优，决策树的剪枝则考虑全局最优
特征选择
特征选择在于选取对训练数据具有分类能力的特征，以提高决策树学习的效率。如果利用一个特征进行分类的结果与随机分类的结果差别不大，则称这个特征没有分类能力，经验上扔掉这样的特征对决策树学习的精度影响不大。特征选择的准则是信息增益或者信息增益比
信息增益
基于信息增益准则的特征选择算法：对训练数据集\(D\)计算每个特征的信息增益，比较大小，选择信息增益最大的特征
熵的定义如下$$H(X) = -\sum_{i=1}^{n}p_i\log p_i$$其中\(P(X=x_i)=p_i, \quad i = 1, 2, \dots, n\)，若\(p_i=0\)则定义\(0\log 0 = 0\)。熵只依赖于\(X\)的分布，与\(X\)的取值无关，所以可将\(X\)的熵记作$$H(p)=-\sum_{i=1}^{n}p_i\log p_i$$熵越大，随机变量的不确定性就越大
例：当随机变量只取两个值\(0\)和\(1\)时，则熵为\(H(p)=-p\log_2 p - (1-p)\log_2 (1-p)\)当\(p=0.5\)时，熵取最大值，随机变量的不确定性最大
条件熵的定义如下$$H(Y|X)=\sum_{i=1}^{n}p_i H(Y|X=x_i)$$其中\(p_i = P(X=x_i)\)，表示给定\(X\)条件下\(Y\)的条件概率分布的熵对\(X\)的数学期望
信息增益表示得知特征\(X\)的信息使得类别\(Y\)的信息不确定性减少的程度，信息增益定义如下
特征\(A\)对训练数据集\(D\)的信息增益\(g(D, A)\)定义为数据集\(D\)的经验熵\(H(D)\)与特征\(A\)给定条件下\(D\)的条件熵\(H(D|A)\)之差$$g(D, A)=H(D)-H(D|A)$$熵\(H(Y)\)与条件熵\(H(D|A)\)之差称为互信息(mutual information)
信息增益算法如下
输入：数据集\(D\)和特征\(A\)
输出：特征\(A\)对数据集\(D\)的信息增益\(g(D, A)\)
- 计算数据集\(D\)的经验熵$$H(D)=-\sum_{k=1}^{K}\dfrac{|C_k|}{|D|}\log_2 \dfrac{|C_k|}{|D|}$$其中\(|C_k|\)表示属于类别\(k\)的样本个数，\(D\)表示样本个数
- 计算特征\(A\)对数据集\(D\)的条件熵\(H(D|A)\)$$H(D|A)=\sum_{i=1}^{n}\dfrac{|D_i|}{|D|}H(D_i)=-\sum_{i=1}^{n}\dfrac{|D_i|}{|D|}\sum_{k=1}^{K}\dfrac{|D_{ik}|}{|D_i|}\log_2 \dfrac{|D_{ik}|}{|D_i|}$$其中\(n\)表示特征取值个数，\(|D_i|\)表示具有特征\(i\)取值样本个数，\(|D_{ik}|\)表示具有特征\(i\)取值的样本中属于类别\(k\)的样本个数
- 计算信息增益$$g(D, A)=H(D)-H(D|A)$$
信息增益比
以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征问题，使用信息增益比对其进行校正
解释：样本总个数是一定的，当某一特征取值较多时候，则分配到每一个特征取值的样本变少，而计算条件熵$$H(D|A)=\sum_{i=1}^{n}\dfrac{|D_i|}{|D|}H(D_i)=-\sum_{i=1}^{n}\dfrac{|D_i|}{|D|}\sum_{k=1}^{K}\dfrac{|D_{ik}|}{|D_i|}\log_2 \dfrac{|D_{ik}|}{|D_i|}$$需要计算某一特征取值为\(i\)时对应的各个类别的概率，而实际用频率，即\(\dfrac{|D_{ik}|}{|D_i|}\)来估计概率，当对应的样本少时，这种估计并不准确（可以类比投硬币实验，实验次数少，估计的结果不准确），存在偏差，使得分布不均匀，而分布不均匀导致计算的熵偏低，进而使得信息增益较大，所以有以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征问题
拓展：如果每一个特征取值下样本数目足够多，则用频率可近似估计概率，每一个特征计算的条件熵基本一样，就不存在所谓的以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征问题
信息增益比\(g_R(D, A)\)定义为信息增益\(g(D, A)\)与训练集\(D\)关于特征\(A\)的值的熵\(H_A(D)\)之比$$g_R(D, A)=\dfrac{g(D, A)}{H_A(D)}$$其中\(H_A(D) = -\sum_{i=1}^{n}\dfrac{|D_i|}{|D|}\log_2 \dfrac{|D_i|}{|D|}\)，\(n\)是特征\(A\)取值的个数
如果\(i\)的取值越多，则\(H_A(D)\)的值越大
决策树的生成
\(\text{ID3}\)算法
输入：训练数据集\(D\)，特征集\(A\)和阈值\(\varepsilon\)
输出：决策树\(T\)
- 若集合\(D\)中所有实例属于同一个类别\(C_k\)，则决策树\(T\)为单节点树，将类别\(C_k\)作为该节点的类标记，返回\(T\)（递归基准条件）
- 若\(A=\varnothing\)，则\(T\)为单节点树，将\(D\)中具有实例数最大的类\(C_k\)作为该节点的类标记，返回\(T\)（递归基准条件）
- 计算\(A\)中各个特征对数据集\(D\)的信息增益，选择信息增益最大的特征\(A_g\)
- 如果\(A_g\)的信息增益小于阈值\(\varepsilon\)，则置\(T\)为单节点树，将\(D\)中实例数最大的类\(C_k\)作为该节点的类标记，返回\(T\)（递归基准条件）
- 否则，对\(A_g\)的每一个可能取值\(a_i\)，依\(A_g=a_i\)将\(D\)分割为若干个非空子集\(D_i\)，将\(D_i\)中实例数最大的类作为标记，构建子节点，由节点及其子节点构成树\(T\)，返回\(T\)
- 对第\(i\)个子节点，以\(D_i\)为训练集，以\(A-\{A_g\}\)为特征集，递归调用\(1\backsim 5\)，得到子树\(T_i\)，返回\(T_i\)
ID3算法的核心是在决策树各个节点上应用信息增益准则选择特征，递归构建决策树，ID3相当于用极大似然法进行概率模型的选择。ID3算法只有树的生成，该算法生成的树容易产生过拟合
\(\text{C4.5}\)算法
输入：训练数据集\(D\)，特征集\(A\)和阈值\(\varepsilon\)
输出：决策树\(T\)
- 若集合\(D\)中所有实例属于同一个类别\(C_k\)，则决策树\(T\)为单节点树，将类别\(C_k\)作为该节点的类标记，返回\(T\)（递归基准条件）
- 若\(A=\varnothing\)，则\(T\)为单节点树，将\(D\)中具有实例数最大的类\(C_k\)作为该节点的类标记，返回\(T\)（递归基准条件）
- 计算\(A\)中各个特征对数据集\(D\)的信息增益比，选择信息增益比最大的特征\(A_g\)
- 如果\(A_g\)的信息增益比小于阈值\(\varepsilon\)，则置\(T\)为单节点树，将\(D\)中实例数最大的类\(C_k\)作为该节点的类标记，返回\(T\)（递归基准条件）
- 否则，对\(A_g\)的每一个可能取值\(a_i\)，依\(A_g=a_i\)将\(D\)分割为若干个非空子集\(D_i\)，将\(D_i\)中实例数最大的类作为标记，构建子节点，由节点及其子节点构成树\(T\)，返回\(T\)
- 对第\(i\)个子节点，以\(D_i\)为训练集，以\(A-\{A_g\}\)为特征集，递归调用\(1\backsim 5\)，得到子树\(T_i\)，返回\(T_i\)
和
ID3算法相似，C4.5在生成树的过程中，用信息增益比来选择特征
决策树剪枝
决策树生成算法递归产生决策树，直到不能继续进行下去为止，容易产生过拟合，因为在学习过程中，过多考虑对训练数据的正确分类，从而构造出复杂的决策树，解决的方法是考虑决策树的复杂度，对已生成的决策树进行剪枝，进而简化决策树模型
决策树的剪枝往往通过极小化决策树整体损失函数实现。设树\(T\)的叶节点个数为\(|T|\)，\(t\)是树\(T\)的叶节点，该叶节点有\(N_t\)个样本，其中第\(k\)类的样本有\(N_{tk}\)个，\(k=1, 2\dots, K\)，\(H_t(T)\)为叶节点\(t\)上的经验熵，\(\alpha \ge 0\)为超参数，决策树的损失函数定义为$$C_{\alpha}(T)=\sum_{t=1}^{|T|}N_tH_t(T)+\alpha |T|$$其中熵为$$H_t(T)=-\sum_{k}\dfrac{N_{tk}}{N_t}\log\dfrac{N_{tk}}{N_t}$$将损失函数的第一项定义为$$C(T)=\sum_{t=1}^{|T|}N_tH_t(T) = -\sum_{t=1}^{|T|}\sum_{k=1}^{K}N_{tk}\log\dfrac{N_{tk}}{N_t}$$则损失函数可以写为$$C_{\alpha}(T)=C(T)+\alpha |T|$$其中\(C(T)\)表示对训练数据的预测误差（如果每一个叶节点可以较好分类，则对应的熵较小，理想情况下熵为\(0\)，即叶节点中只有一个类别），即模型对训练数据的拟合程度，\(|T|\)表示模型复杂度，\(\alpha\)较大，则促使选择简单模型，\(\alpha\)较小，促使选择复杂模型
剪枝就是当\(\alpha\)确定时，选择使得损失函数最小的模型，即损失函数最小的子树。决策树生成只考虑提高信息增益（或者信息增益比）来对训练数据进行拟合，而决策树的剪枝通过优化损失函数考虑减小模型复杂度，决策树生成学习局部模型，决策树剪枝学习整体模型
决策树剪枝算法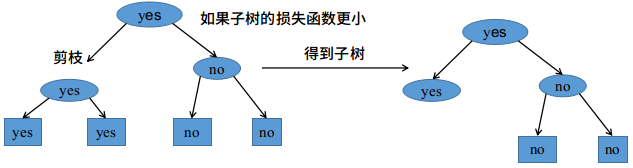
输入：生成算法产生的整个树\(T\)，参数\(\alpha\)
输出：剪枝后的子树\(T_{\alpha}\)
- 计算每个节点的经验熵
- 递归从树的叶节点向上回缩
设一组叶节点回缩到其父节点之前和之后的整体树分别为\(T_B\)和\(T_A\)，其对应的损失函数分别为\(C_{\alpha}(T_B)\)和\(C_{\alpha}(T_A)\)，若$$C_{\alpha}(T_A)\le C_{\alpha}(T_B)$$则进行剪枝，即将父节点变为新的叶节点 - 返回第\(2\)步，知道不能继续为止，得到损失函数最小的子树\(T_{\alpha}\)
第\(2\)步中只考虑两个树的损失函数之差，其计算可以在局部进行，因此，决策树剪枝算法可以通过动态规划算法实现
\(\text{CART}\)算法
分类与回归树(classification and regression tree, CART)是在给定输入随机变量\(X\)的条件下输出随机变量\(Y\)的条件概率分布的学习方法。CART假设决策树是二叉树，CART算法由以下两步组成
- 决策树生成：基于训练数据集生成决策树，生成的决策树要尽量大
- 决策树剪枝：用验证集对已生成的树进行剪枝，并选择最优子树，用损失函数最小作为剪枝标准
\(\text{CART}\)生成
CART决策树的生成就是递归构建二叉决策树的过程。对回归树用平方误差最小化准则，对分类树用基尼指数(Gini index)最小化准则进行特征选择。
回归树生成
假设\(X\)与\(Y\)分别为输入和输出变量，并且\(Y\)是连续变量，给定训练数据集$$D=\{(x_1, y_1), (x_2, y_2), \dots, (x_N, y_N)\}$$考虑如何生成回归树。一棵回归树对应输入空间（特征空间）的一个划分及在划分单元上的输出值。假设将输入空间划分为\(M\)个单元\(R_1, R_2, \dots, R_M\)，且在每个单元\(R_m\)上有一个固定的输出值\(c_m\)，回归树可以表示为$$f(x)=\sum_{m=1}^{M}c_mI(x\in R_m)$$当输入空间划分确定时，可用平方误差\(\sum_{x_i\in R_m}(y_i - f(x_i))^2\)表示回归树对训练集的误差，基于平方误差最小准则求解每个单元上的最优输出值。可知，单元\(R_m\)上的\(c_m\)最优输出值\(\hat{c_m}\)是\(R_m\)上所有输入\(x_i\)对应输出\(y_i\)的均值，即$$\hat{c_m} = \text{ave}(y_i|x_i\in R_m)$$问题转为如何对输入空间划分。采用启发式的方式，选择第\(j\)个变量\(x^{j}\)（也就是第\(j\)个特征）和其取值\(s\)作为切分变量和切分点，定义两个区域$$R_1(j, s) = \{x|x^{j}\le s\}\quad 和\quad R_2(j, s) = \{x|x^{j} > s\}$$然后寻找最优切分变量\(j\)（第\(j\)个特征）和对应的最优切分点\(s\)，即求解$$\mathop{\text{min}}\limits_{j, s}\big [\mathop{\text{min}}\limits_{c_1} \sum_{x_i \in R_1 (j, s)}(y_i - c_1)^2 + \mathop{\text{min}}\limits_{c_2}\sum_{x_i \in R_2 (j, s)}(y_i - c_2)^2\big]$$对固定输入变量\(j\)（第\(j\)个特征）可以找到最优切分点\(s\)$$\hat{c_1}=\text{ave}(y_i|x_i\in R_1(j, s))\quad 和 \quad \hat{c_2}=\text{ave}(y_i|x_i\in R_2(j, s))$$遍历所有输入变量(特征），找到最优切分变量（特征）\(j\)，构成一个对\((j, s)\)，根据此将输入空间分为两个区域。对每个区域重复上述划分过程，直到满足停止条件，生成一颗回归树，这样的回归树称为最小二乘回归树。
最小二乘回归树生成算法
输入：训练数据集\(D\)
输出：回归树\(f(x)\)
在训练数据集所在的输入空间（特征空间），递归地将每个区域划分为两个子区域，并决定每个子区域的输出值，构建二叉决策树
- 选择最优切分变量\(j\)（第\(j\)个特征)和切分点\(s\)，求解$$\mathop{\text{min}}\limits_{j, s}\big [\mathop{\text{min}}\limits_{c_1} \sum_{x_i \in R_1 (j, s)}(y_i - c_1)^2 + \mathop{\text{min}}\limits_{c_2}\sum_{x_i \in R_2 (j, s)}(y_i - c_2)^2\big]$$遍历变量\(j\)，对固定切分变量\(j\)扫描切分点\(s\)选择使得上式达到最小值的对\((j, s)\)
- 用选定的对\((j, s)\)划分区域，并决定相应的输出值$$R_1(j, s)=\{x|x^j \le s\}, \quad R_2(j, s)=\{x|x^j > s\}\\\hat{c_1}=\dfrac{1}{N_m}\sum_{x_i\in R_m(j, s)}y_j, \quad x\in R_m, \quad m = 1, 2$$
- 继续对两个子区域重复\(1\backsim 2\)，直到满足停止条件
- 将输入空间划分为\(M\)个区域\(R_1, R_2, \dots, R_M\)，生成决策树$$f(x) = \sum_{m=1}^{M}\hat{c_m}I(x\in R_m)$$
分类树的生成
基尼指数：分类问题中，假设有\(K\)个类别，样本点属于第\(k\)个类的概率为\(p_k\)，则概率分布的基尼指数为$$\text{Gini}(p)=\sum_{k=1}^{K}p_k(1-p_k)=1-\sum_{k=1}^{K}p_k ^2$$对于二分类问题，若样本点属于第一个类的概率为\(p\)，则概率分布的基尼指数为$$\text{Gini}(p)=2p(1-p)$$对于给定的样本集合\(D\)，其基尼指数为$$\text{Gini}(D)=1-\sum_{k=1}^{K}\big(\dfrac{|C_k|}{|D|}\big)^2$$其中\(C_k\)表示属于第\(k\)类的样本子集，\(K\)为类别个数
如果样本集合\(D\)根据特征\(A\)是否取某一可能值\(a\)被分为\(D_1\)和\(D_2\)两部分，即$$D_1=\{(x, y)\in D|A(x)=a\}, \quad D_2 = D-D_1$$则在特征\(A\)的条件下，集合\(D\)的基尼指数定义为$$\text{Gini}(D, A)=\dfrac{|D_1|}{|D|}\text{Gini}(D_1)+\dfrac{|D_2|}{|D|}\text{Gini}(D_2)$$基尼指数\(\text{Gini}(D)\)表示集合\(D\)的不确定性，\(\text{Gini}(D, A)\)表示经\(A=a\)分割后集合\(D\)的不确定性。基尼指数越大，样本集合的不确定性就越大，与熵相似
\(\text{CART}\)分类树生成算法
输入：训练数据集\(D\)，停止条件
输出：\(\text{CART}\) 决策树
根据训练数据，从根节点开始，递归对每个节点进行以下操作，构建二叉决策树
- 设节点的训练数据集为\(D\)，计算现有特征对该数据集的基尼指数。此时，对每一个特征\(A\)，对其每一个取值\(a\)，根据样本点对\(A=a\)的测试为“是”或“否”（二叉树）将\(D\)分为\(D_1\)和\(D_2\)，计算\(A=a\)的基尼指数，即\(\text{Gini}(D, A)\)
- 在所有可能的特征\(A\)和它们所有可能切分点\(a\)中，选择基尼指数最小的特征，及对应的切分点最为最优特征与最优切分点。根据此最优特征和最优切分点，从当前节点生成两个子节点，将训练集根据此特征分配到两个子节点中
- 对两个子节点递归调用\(1\backsim 2\)，直到满足停止条件
- 生成\(\text{CART}\)决策树
算法停止条件：节点中样本个数小于预定阈值，样本集的基尼指数小于阈值（样本基本属于同一个类），或者没有更多特征
\(\text{CART}\)剪枝
CART剪枝算法从“完全生长”的决策树的底端剪去一些子树，使模型变得简单，提高模型的泛化能力。由两步组成：首先从生成树\(T_0\)底端开始不断剪枝，直到\(T_0\)的根节点，构成一个子树序列\(\{T_0, T_1, \dots, T_n\}\)；然后通过交叉验证法在独立的验证集上对子树序列进行测试，选择最优子树
剪枝形成一个子树序列
在剪枝过程中，计算子树的损失函数$$C_{\alpha}(T)=C(T)+\alpha |T|$$其中，\(T\)为任意子树，\(C(T)\)为对训练数据的预测误差（例如基尼指数），\(|T|\)为子树的叶节点个数，\(\alpha \ge 0\)为超参数。对于固定的\(\alpha\)，一定存在使损失函数\(C_{\alpha}(T)\)最小的子树，表示为\(T_{\alpha}\)。这样的子树\(T_{\alpha}\)是唯一的
Breiman等人证明：可以用递归的方法对树进行剪枝，将\(\alpha\)从小增大，\(0=\alpha_0 < \alpha_1 < \dots < \alpha_n < \infty\)，产生一系列的区间\([\alpha_i, \alpha_{i+1}), \quad, i = 0, 1, \dots, n\)。剪枝得到的子树序列对应着区间\(\alpha \in [\alpha_i, \alpha_{i+1}), \quad, i = 0, 1, \dots, n\)的最优子树序列\(\{T_0, T_1, \dots, T_n\}\)，序列中的子树是嵌套的
具体来说，从整体树\(T_0\)开始剪枝，对\(T_0\)的任意内部节点\(t\)，以\(t\)为单节点树的损失函数为$$C_{\alpha}(t)=C(t)+\alpha$$以\(t\)为根节点的子树\(T_t\)的损失函数为$$C_{\alpha}(T_t)=C(T_t)+\alpha |T_t|$$当\(\alpha = 0\)或者\(\alpha\)充分小时，有$$C_{\alpha}(T_t) < C_{\alpha}(t)$$当\(\alpha\)增大时，存在某一\(\alpha\)有$$C_{\alpha}(T_t)=C_{\alpha}(t)$$继续增大\(\alpha\)，有$$C_{\alpha}(T_t) > C_{\alpha}(t)$$只要\(\alpha = \dfrac{C(t)-C(T_t)}{|T_t|-1}\)，\(T_t\)与\(t\)有相同的损失函数值，而\(t\)的节点少，所有\(t\)比\(T_t\)更加可取，对\(T_t\)进行剪枝
为此，对\(T_0\)内部的每一个节点\(t\)计算$$g(t)=\dfrac{C(t)-C(T_t)}{|T_t|-1}$$其表示剪枝后整体损失函数减少的程度。在\(T_0\)中剪去\(g(t)\)最小的\(T_t\)得到的子树作为\(T_1\)，同时将最小的\(g(t)\)设为\(\alpha_1\)。\(T_1\)为区间\([\alpha_1, \alpha_2)\)的最优子树。如此进行下去，知道根节点，在这一过程中不断增加\(\alpha\)的值，产生新的区间
理解：上述公式\(g(t)\)表示剪枝的阈值，即对于某一节点\(t\)，当总体损失函数中参数\(\alpha = g(t)\)时候，剪和不剪总体损失函数是一样的，这时候如果增大\(\alpha\)，就有不剪枝的损失函数大于剪枝的。也即当\(\alpha\)大于\(g(t)\)时候，应该剪去，因为剪去会使得整体损失函数减小，但当\(\alpha\)小于\(g(t)\)时不应该剪去，剪枝会使得损失函数变大
对于同一棵树节点，其\(\alpha\)都是一样的，当\(\alpha\)不断增大时，总会有某棵子树该剪，其他不应该剪，即\(\alpha\)超过了某个节点的\(g(t)\)，但没超过其它节点的\(\alpha\)
在剪枝得到的子树序列\(T_0, T_1, \dots, T_n\)通过交叉验证选取最优子树
利用验证集，测试子树序列\(T_0, T_1, \dots, T_n\)中各棵子树的平方误差或者基尼指数。平方误差或者基尼指数最小的决策树认为是最优的决策树，在每一棵子树\(T_1, T_2, \dots, T_n\)中，都对应着一个参数\(\alpha_1, \alpha_2, \dots, \alpha_n\)，因此，当最优子树\(T_k\)确定时，对应的\(\alpha_k\)就确定了，得到最优决策树\(T_{\alpha}\)
\(\text{CART}\)剪枝算法
输入：\(\text{CART}\)生成算法产生的决策树\(T_0\)
输出：最优决策树\(T_{\alpha}\)
- 设\(k=0, \quad T = T_0\)
- 设\(\alpha = +\infty\)
- 自下而上对各内部节点\(t\)计算\(C(T_t)\)，\(|T_t|\)以及$$\begin{equation}\begin{aligned}g(t)&=\dfrac{C(t)-C(T_t)}{|T_t|-1}\\\alpha&=\text{min}(\alpha, g(t))\end{aligned}\end{equation}$$其中\(T_t\)表示以\(t\)为根节点的子树，\(C(T_t)\)是对训练数据集的预测误差，\(|T_t|\)是\(T_t\)的叶节点个数
- 对\(g(t)=\alpha\)的内部节点\(t\)进行剪枝，并对叶节点\(t\)以多数表决法决定其类别，得到树\(T\)
- 设\(k=k+1\)，\(\alpha_k = \alpha\)， \(T_k = T\)
- 如果\(T_k\)不是由根节点及两个叶节点构成的树，返回到第\(2\)步，否则令\(T_k = T_n\)
- 采用交叉验证法在子树序列\(T_0, T_1, \dots, T_n\)中选择最优子树\(T_{\alpha}\)
\(\text{ID3}\), \(\text{C4.5}\)和\(\text{CART}\)比较
首先，ID3采用信息增益作为评价标准，但是会倾向于取值较多的特征，因为信息增益反映给定条件后不确定性减少程度，特征值越多，意味着确定性越高，信息增益越大（具体可参照之前C4.5下面的解释）。C4.5是对ID3的改进，引入信息增益比，其在一定程度上对取值较多的特征进行惩罚。
从样本类型角度，ID3只能处理离散型变量，C4.5和CART都可以处理连续型变量
从应用角度，ID3和C4.5只能用于分类任务，而CART可以用于分类（基尼指数）也可以用于回归（最小平方误差准则）
从实现细节，优化过程，ID3对缺失值敏感，而C4.5和CART可以对缺失值进行不同方式处理。ID3和C4.5可以在每个节点产生多个分支（离散特征），且每个特征层级之间不能复用，而CART每个节点只会产生两个分支，最后形成一颗二叉树，且每个特征可以重复使用（可以继续分）。ID3和C4.5通过剪枝来权衡树的准确性和泛化能力，而CART树直接利用全部数据发现所有可能树结构进行对比（交叉验证）
建议：小样本用
C4.5，大样本用CART。增益比准则对取值数目较少的特征有所偏好，因此C4.5算法并不是直接选择增益比最大的属性作为分支标准，而是先从候选属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的
缺失值处理
缺失值问题可以从三个方面来考虑
- 在选择分裂特征的时候，训练样本存在缺失值，如何处理？
假如你使用ID3算法，那么选择分类特征时，就要计算所有属性的熵增。假设\(10\)个样本，特征是\(a,b,c\)。在计算\(a\)特征熵时发现，第\(10\)个样本的\(a\)特征缺失，那么就把第\(10\)个样本去掉，前\(9\)个样本组成新的样本集，在新样本集上按正常方法计算\(a\)特征的熵增。然后结果乘\(0.9\)（新样本占原始样本的比例），就是\(a\)特征最终的熵
- 分类属性选择完成，对训练样本分类，发现特征缺失怎么办？
比如该节点是根据\(a\)特征划分，但是待分类样本\(a\)特征缺失。假设\(a\)特征离散，有\(1,2\)两种取值，那么就把该样本分配到两个子节点中去，但是权重由\(1\)变为相应离散值个数占样本的比例。计算错误率的时候，注意，不是每个样本都是权重为\(1\)，存在分数
- 训练完成，给测试集样本分类，有缺失值怎么办？
分类时，如果待分类样本有缺失变量，而决策树决策过程中没有用到这些变量，则决策过程和没有缺失的数据一样；否则，如果决策要用到缺失变量，决策树也可以在当前节点做多数投票来决定（选择样本数最多的特征值方向）
参考：统计学习方法（第二版）–李航
https://www.zhihu.com/question/34867991