集成学习
Voting Classifiers
假如有几个训练好的分类器，例如：\(\text{Logistic Regression classifier}\)，\(\text{SVM classifier}\)，随机森林和\(\text{K-Nearest}\)等等，每一个实现大约\(80\%\)分类准确率。创建一个更好的分类器的简单方法是根据多数投票法(the most votes)集成(aggregate)每个分类器的预测输出。基于多数投票的方法称为\(\text{hard voting classifier}\)
基于投票集成的分类方法(voting classifiers)经常得到比单一最好的分类器更好的分类准确率。事实上，即使每个单一的分类器是弱分类器(weak learner)（即其仅仅比随机猜测好点），通过集成可以得到强的分类器，假如有足够多的弱分类器且每个都是独立的
解释：以投掷硬币为例。假如有一个不均匀硬币，其正面出现的概率为\(51\%\)，反面出现的概率为\(49\%\)，则投掷\(1000\)次后，一般情况下会得到大约\(510\)次正面，\(490\)次反面，也就是正面占多数（基于多数投票法会得到正的结果）。通过数学计算，可以得到投掷\(1000\)次后，最后获得正面结果（基于多数投票法）大约\(75\%\)左右，投掷的总次数越多，得到正面的概率越大（投掷\(10000\)得到结果接近\(97\%\)）。因为由于大数定律可知，投掷的次数足够多时，基于频率估计的概率值和真实值比较接近。在本例中，投掷的次数越多，每次投掷出现正面的概率为接近\(51\%\)
类比：如果集成包含\(1000\)个独立的分类器，每一个准确率大约\(51\%\)，则基于多数投票法可以达到约\(75\%\)的准确率，前提条件是各个分类器是完全独立的，产生不相关的错误(making uncorrelated errors)，实际中由于每个分类器在相同的训练集上训练，很可能产生相同类型的错误，使得对于错误类别产生多数相同结果，影响性能。
建议：当各个分类器是独立的时候，集成方法产生较好的结果。因此一种方法获得独立的分类器是训练不同的算法（例如SVM，决策树等等），这增加各个分类器产生不同类型错误的机会，改善集成方法的性能
如果所有的分类器可以估计类概率值，可以使用软投票法(soft voting)，即对于每个样本的每个类别的输出概率值对所有分类器取平均，作为最后的结果。软投票法一般获得更好的结果比起硬投票法，因为它给了更高的权重对于有把握的结果（概率值大）
Bagging and Pasting
获取独立分类器一般有两种方法：
- 使用不同的训练算法（例如：SVM， LR， 决策树等等），上面已经讨论
- 使用相同的训练算法，但是训练它们在整个训练集的不同的随机子集上。如果采用有放回方法获取子集样本，则称为bagging，当采用无放回方法获取子集样本，则称为pasting
每一个独立的预测器有更高的偏差比起在原始的训练集上训练的样本（样本少，学习到的偏差也就大），但是通过集成减少方差和偏差。一般情况下，和在原始训练集上训练的单个预测器比，集成学习得到相似的偏差，但是有更低的方差
对于bagging and pasting，预测器可以并行训练，可以较好处理大样本，这是其优势
Out-of-Bag Evaluation
对于bagging（有放回抽样），一些样本可能被采用几次，一些样本可能从来没有被采样。对于每个预测器，采用\(m\)次得到\(m\)个训练样本，有平均大约\(63\%\)的样本会被采用到（随着\(m\)的增大，比例接近\(1-e^{-1}\approx 63.212\%\)），剩下的\(37\%\)不会被采样到，称不被采样的\(37\%\)样本为out-of-bag(oob)
由于一个预测器不会看到oob样本，因此可以用此样本评估预测器，不需要单独划分验证集或者使用交叉验证。也可以评估集成方法本身，通过平均每个预测器的oob估计值
Random Patches and Random Subspaces
可以直接对特征进行采样（之前是对样本实例进行采样），这样每个预测器被训练在输入特征的一个随机子集上，对于处理高维数据（例如：图像），这特别有用。如果对训练实例（样本）和特征同时采样，称为Random Patches方法。如果只是对特征进行采样称为Random Subspaces方法
随机森林
随机森林是决策树的集成，通常通过bagging方法训练（有时候是pasting)。随机森林算法在生成树过程中引入额外的随机性，其划分节点并不是选择最好的特征，而是在一个随机特征子集上选择最好特征，这得到更大的树的差异性，导致更高的偏差（对于单个树而言）和更低的方差（对于整体，也就是集成），进而产生一个更好的模型
Extra-Trees
对于常规的随机森林，在每一个节点仅仅一个随机特征子集被用来划分。使得树更具有随机性是可能的，通过对每一个特征使用一个随机阈值，而不是选择最好的阈值（决策树采用的），这样的方法称为Extremely Randomized Trees集成。这导致更多的偏差（对于单个树而言）和低的方差（对于整体，也就是集成）。Extra-Trees训练更快比起常规的随机森林（在每个节点选择最好的特征阈值）。
注意：并不能说明Extra-Trees和常规随机森林哪个更好，通常情况下，通过交叉验证比较两种方法
特征重要性
对于决策树，重要的特征很可能出现的更靠近树根，不重要的特征经常出现在靠近叶节点。因此，特征重要性的估计可以通过计算其出现在随机森林中所有树中的平均深度。随机森林是非常方便的对于去快速理解什么特征重要，可以用于特征选择
Boosting
大多数提升方法(boosting)是按照序列(sequentially)训练预测器，每一个尝试修正其前任(predecessor)。大多数提升方法都是改变训练数据的概率分布（训练数据的权值分布），针对不同的训练数据分布调用弱学习算法学习一系列弱分类器
AdaBoost
对于AdaBoost算法，提高那些被前一轮弱分类器错误分类样本权重，从而降低那些被正确分类的样本权重，这样一来，那些没有得到正确分类的数据，由于其权重加大而受到后一轮弱分类器的更大关注。于是问题被一系列的弱分类器分而治之。
一旦所有的弱分类器被训练完成，AdaBoost采用加权多数表决方法进行组合。具体地，加大分类误差率小的弱分类器的权值，使其在表决中起到较大作用，减小分类误差率大的弱分类器权值，使其在表决中起较小的作用
算法
输入：训练数据集\(T=\{(x_1, y_1), (x_2, y_2), \dots, (x_N, y_N)\}\)，其中\(x_i\in R^n\)，\(y_i\in \{-1, +1\}\)；弱分类算法
输出：最终分类器\(G(x)\)
- 初始化训练数据的权值分布$$D_1 = (\omega_{11}, \omega_{12}, \dots, \omega_{1N}), \quad \omega_{1i}=\frac{1}{N}$$
- 对于\(m=1, 2, \dots, M\)
- 使用具有权值分布\(D_m\)的训练数据学习，得到基本分类器\(G_m(x)\)
- 计算\(G_m(x)\)在训练数据集上的分类误差率$$e_m = \sum_{i=1}^{N}P(G_m (x_i) \not = y_i) = \sum_{i=1}^{N}\omega_{mi}I(G_m (x_i) \not = y_i)$$
- 计算\(G_m(x)\)的系数$$\alpha_m = \dfrac{1}{2}\ln\dfrac{1-e_m}{e_m}$$
- 更新训练数据集的权值分布$$D_{m+1} = (\omega_{m+1, 1}, \dots, \omega_{m+1, i}, \dots, \omega_{m+1, N}\\\omega_{m+1, i} = \dfrac{\omega_{mi}}{Z_m}e^{-\alpha_m y_iG_m(x_i)}, \quad i = 1, 2, \dots, N$$其中\(Z_m\)是规范化因子$$Z_m = \sum_{i=1}^{N}\omega_{mi}e^{-\alpha_m y_i G_m(x_i)}$$其使得\(D_{m+1}\)是一个概率分布
- 构建基本分类器线性组合$$f(x) = \sum_{m=1}^{M}\alpha_mG_m(x)$$得到最终的分类器$$\begin{equation}\begin{aligned}G(x)&=\text{sign}(f(x))\\&= \text{sign}\Big(\sum_{m=1}^{M}\alpha_mG_m(x)\Big)\end{aligned}\end{equation}$$
对AdaBoost算法说明如下：
- 步骤1中，假设训练数据集具有均匀的权值分布，即每个训练样本在基本分类器的学习中作用相同，保证第一步能够在原始数据集上学习基本分类器\(G_1(x)\)
- 步骤2中，AdaBoost反复学习基本分类器，在每一轮\(m=1, 2, \dots, M\)顺序执行以下操作
- 使用当前分布\(D_m\)加权的训练数据集，学习基本分类器\(G_m(x)\)
- 计算基本分类器\(G_m(x)\)在加权训练数据集上的分类误差率$$\begin{equation}\begin{aligned}e_m &= \sum_{i=1}^{N}P(G_m(x_i) \not = y_i)\\&=\sum_{G_m(x_i)\not = y_i}\omega_{mi}\end{aligned}\end{equation}$$其中\(\omega_{mi}\)表示第\(m\)轮中第\(i\)个实例的权值，有\(\sum_{i=1}^{N}\omega_{mi}=1\)
- 计算基本分类器\(G_m(x)\)的系数\(\alpha_m\)，\(\alpha_m\)表示\(G_m(x)\)在最终分类器中的重要性。根据算法第2步中计算\(\alpha_m\)的公式可知，当\(e_m\le \dfrac{1}{2}\)时，\(\alpha_m\ge 0\)，且\(\alpha_m\)随着\(e_m\)的减小而增大，所以分类误差率越小的基本分类器在最终的分类器中作用越大
- 更新训练数据的权值分布$$\begin{equation}\omega_{m+1,i}=\begin{cases}\dfrac{\omega_{mi}}{Z_m}e^{-\alpha_m}, &G_m(x_i)=y_i\\\dfrac{\omega_{mi}}{Z_m}e^{\alpha_m}, &G_m(x_i)\not =y_i\end{cases}\end{equation}$$可知被基本分类器\(G_m(x)\)误分类样本的权值得以扩大，被正确分类样本权值得以缩小，因此误分类样本在下一轮学习中起到更大作用。不改变训练数据集，只是改变训练数据的权值分布，使得训练数据在基本分类器的学习中起不同的作用，是AdaBoost的一个特点
说明：由于基本分类器是弱分类器（比随机猜测好点），因此其分类误差率\(e_m\le \dfrac{1}{2}\)，得到\(\alpha_m\ge 0\)- 步骤3中，线性组合\(f(x)\)实现\(M\)个基本分类器的加权表决，系数\(\alpha_m\)表示基本分类器\(G_m(x)\)的重要性，注意这里\(\alpha_m\)之和并不是\(1\)，\(f(x)\)的绝对值越大，表示分类的置信度越高，利用基本分类器的线性组合得到最终分类器是AdaBoost的另一个特点
AdaBoost最基本的性质是它在学习过程中不断减小训练误差，即在训练数据集上的分类误差率（证明参考统计学习方法）
AdaBoost算法是前向分布加法算法的特例，模型是基本分类器组成加法模型，损失函数是指数函数。
前向分布算法思想：因为学习是加法模型，如果能够从前向后，每一步只学习一个基函数及其系数，逐步逼近最终加法模型目标函数，可以简化优化的复杂度
提升树
提升树是以分类树或回归树为基本分类器的提升方法，其被认为是统计学习中性能最好的方法之一
提升树算法
提升树采用前向分布算法，和加法模型。首先确定初始提升树\(f_0(x)=0\)，第\(m\)步的模型为$$f_m(x)=f_{m-1}(x)+T(x;\theta_m)$$其中\(T(x;\theta_m)\)表示决策树，\(\theta_m\)是决策树参数，\(f_{m-1}(x)\)表示当前模型，通过经验风险极小化确定确定下一颗决策树的参数\(\theta_m\)$$\hat{\theta_m}=\text{arg}\mathop{\text{min}}\limits_{\theta_m}\sum_{i=1}^{N}L(y_i, f_{m-1}(x_i)+T(x_i;\theta_m))$$由于树的线性组合可以很好拟合训练数据，即使数据中的输入和输出之间的关系很复杂也是如此，因此提升树是一个高功能提升算法
对于二分类问题，提升树算法只需要将AdaBoost算法中基本分类器限制为二类分类决策树即可，下面主要讨论对于回归问题的提升树
已知训练数据集\(T=\{(x_1, y_1), (x_2, y_2), \dots, (x_N, y_N)\}\)，\(x_i\in R^n, \quad y_i\in R\)，如果将输入空间划分为\(J\)个不相交的区域\(R_1, R_2, \dots, R_J\)，且在每个区域上确定输出的常量\(c_j\)，那么树可以表示为$$T(x;\theta)=\sum_{j=1}^{J}c_jI(x\in R_j)$$其中参数\(\theta = \{(R_1, c_1), (R_2, c_2), \dots, (R_J, c_J)\}\)，\(J\)是树的复杂度，即叶节点的个数
回归问题提升决策树使用以下前向分布算法$$\begin{equation}\begin{aligned}&f_0(x)=0\\&f_m(x)=f_{m-1}(x)+T(x;\theta_m), \quad m=1, 2, \dots, M\\&f_M(x)=\sum_{m=1}^{M}T(x;\theta_m)\end{aligned}\end{equation}$$在前向分布算法的第\(m\)步，给定当前模型\(f_{m-1}(x)\)，求解$$\hat{\theta_m}=\text{arg}\mathop{\text{min}}\limits_{\theta_m}\sum_{i=1}^{N}L(y_i, f_{m-1}(x_i)+T(x_i;\theta_m))$$得到\(\hat{\theta_m}\)，即第\(m\)棵树的参数
当采用平方误差损失函数时$$L(y, f(x))=(y-f(x))^2$$其损失变为$$\begin{equation}\begin{aligned}L(y,f_{m-1}(x)+T(x;\theta_m))&=[y-f_{m-1}(x)-T(x;\theta_m)]^2\\&=[r-T(x;\theta_m)]^2\end{aligned}\end{equation}$$其中\(r=y-f_{m-1}(x)\)表示当前模型\(f_{m-1}(x)\)拟合数据的残差(residual)，因此对于回归问题的提升树，只需要简单拟合当前模型的残差
算法
输入：训练数据集\(T=\{(x_1, y_1), (x_2, y_2), \dots, (x_N, y_N)\}\)，\(x_i\in R^n, \quad y_i\in R\)
输出：提升树\(f_M(x)\)
- 初始化\(f_0(x)=0\)
- 对\(m=1, 2, \dots, M\)
- 计算残差$$r_{mi}=y_i - f_{m-1}(x_i), \quad i = 1, 2, \dots, N$$
- 拟合残差\(r_{mi}\)学习一个回归树，得到\(T(x;\theta_m)\)
- 更新\(f_m(x)=f_{m-1}(x)+T(x;\theta_m)\)
- 得到回归提升树$$f_M(x)=\sum_{m=1}^{M}T(x;\theta_m)$$
平方误差损失\(L(y,f_M(x))=\sum_{i=1}^{N}(y_i-f_M(x_i))^2\)满足要求可以退出
梯度提升
提升树利用加法模型和前向分布算法实现学习的优化过程。当损失函数是平方损失或者指数损失，每一步优化很简单。对于一般的损失函数，每一步的优化并不容易，针对此问题，Freidman提出梯度提升(gradient boosting)算法。这是利用最速下降的近似方法，其关键是利用损失函数的负梯度在当前模型的值$$-\Big[\dfrac{\partial{L(y,f(x_i))}}{\partial{f(x_i)}}\Big]_{f(x)=f_{m-1}(x)}$$作为回归提升树中的残差的近似值，拟合一个回归树
梯度提升算法
输入：训练数据集\(T=\{(x_1, y_1), (x_2, y_2), \dots, (x_N, y_N)\}\)，\(x_i\in R^n, \quad y_i\in R\)，损失函数\(L(y, f(x))\)
输出：回归树\(\widehat{f(x)}\)
- 初始化$$f_0(x)=\text{arg}\mathop{\text{min}}\limits_{c}\sum_{i=1}^{N}L(y_i, c)$$
- 对于\(m=1, 2, \dots, M\)
- 对\(i=1, 2, \dots, N\)，计算$$r_{mi}=-\Big[\dfrac{\partial{L(y,f(x_i))}}{\partial{f(x_i)}}\Big]_{f(x)=f_{m-1}(x)}$$
- 对\(r_{mi}\)拟合一个回归树，得到第\(m\)棵树的叶节点区域\(R_{mj}, \quad j=1, 2, \dots, J\)
- 对\(j=1, 2, \dots, J\)，计算$$c_{mj}=\text{arg}\mathop{\text{min}}\limits_{c}\sum_{x_i\in R_{m,j}}L(y_i, f_{m-1}(x_i)+c)$$
- 更新$$f_m(x)=f_{m-1}(x)+\sum_{j=1}^{J}c_{mj}I(x \in R_{mj})$$
- 得到回归树$$\widehat{f(x)}=f_M(x)=\sum_{m=1}^{M}\sum_{j=1}^{J}c_{mj}I(x\in R_{mj})$$
算法第1步，估计损失函数极小化的常数值，是一个只有根节点的树，第2步首先计算损失函数负梯度在当前模型的值，作为残差的近似值
Stacking
基本思想：并不是使用trivial functions（例如：hard voting）集成所有预测器的预测结果，而是训练一个模型去执行集成（也就是将其他基类预测器结果作为输入），下图是一个回归任务的最后结果集成说明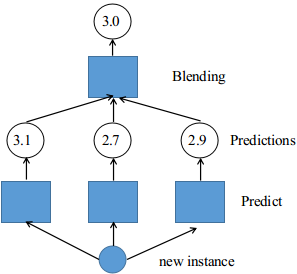
底层每个基本预测器产生一个输出，并作为上层的预测器(blending)的输入，最后给出结果
一种常用的方法训练blender是使用hold-out set
- 首先训练数据被划分为两个子集
- 第一个子集被用来训练在第一层的预测器（基本预测器），如下图所示
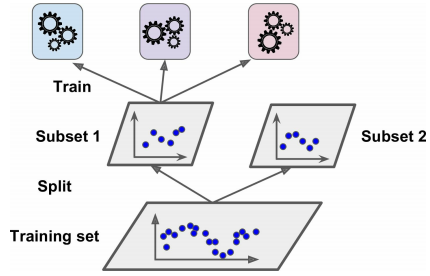
- 将第二个子集作为训练好的第一层基本预测器的输入，并将其输出作为blender的输入，如下图所示。根据第一层的输出创建一个新的训练数据集（图中新的训练集是3维的），作为blender的训练数据集
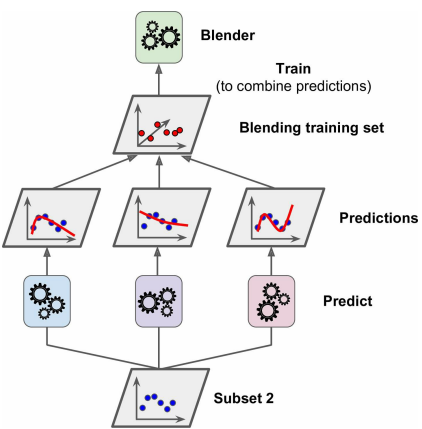
实际中可以用这种方式训练几个不同的blender（例如：一个使用LR，另一个使用随机森林等等），因此我们可以得到一层的blenders，需要将训练数据划分为\(3\)个子集，第一个子集被用来训练第一层的基本预测器；第二个子集被用来创建新的训练数据，用于训练第二层（将第一层的输出作为输入）；第三个子集被用来创建一个新的训练数据用于训练第三层（使用第二层的输出作为输入）下图是说明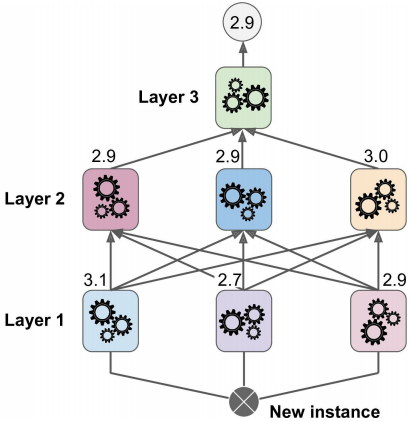
参考：Hands-On Machine Learning with Scikit-Learning & TensorFlow
统计学习方法（第二版）