梯度消失和梯度爆炸
在反向传播算法中，在计算的梯度从输出层到输入层的传播过程中，梯度经常变得越来越小，这种称为梯度消失。相反，在梯度传播过程中，梯度变得越来越大，导致模型发散，这种称为梯度爆炸（在RNN中最可能遇到）。一般情况下，神经网络经常遭遇不稳定的梯度，即不同的层可能以不同的速度学习
缓解方法
Xavier和He初始化
由于不想信号在网络传播过程中（前向传播和反向传播）死掉或者出现爆炸或者饱和，我们需要每一层的输出和输入的方差相等，同样在反向传播中，每一层输入和输出的梯度方差也应该相等。实际中由于每一层的输入和输出的神经元不同，这很难实现，一种折中的方法是使用如下的初始方法，如下图所示
其中\(\text{n}_{\text{inputs}}\)和\(\text{n}_{\text{outputs}}\)是某一层的输入和输出连接数
非饱和的激活函数
ReLu激活函数存在对于正的值不会出现饱和现象和计算速度块等优点。但是也存在缺点：某些神经元在训练过程中可能死亡（输出为0，导数也是0）
为了解决上述ReLu函数的缺点，可以使用ReLu激活函数的变体。leaky ReLu激活函数定义为\(\text{LeakyReLU}_{\alpha}(z) = \max(\alpha z, z)\)如下图所示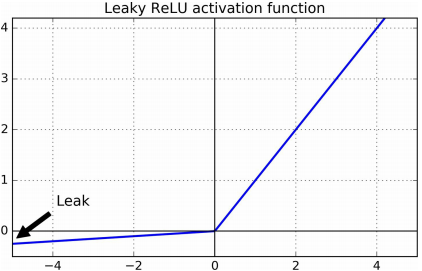
其中超参数\(\alpha\)可以随机选择，设置为固定值，也可以作为学习的参数
另一个变体是exponential linear unit(ELU)，定义如下$$\begin{aligned}\text{ELU}_{\alpha}(z) = \begin{cases}\alpha (\text{exp}(z)-1) \quad &if \quad z < 0\\ z \quad &if \quad z\ge 0\end{cases}\end{aligned}$$如下图所示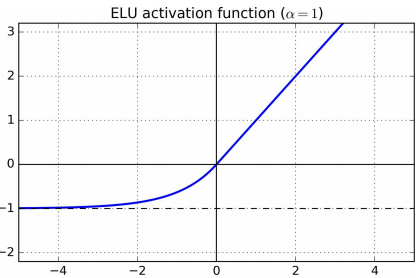
其梯度更加平滑。主要缺点是计算（前向和反向）比ReLu慢。
建议：选择激活函数ELU > leakyReLU > ReLu > tanh > sigmoid
Batch Normalization
尽管使用非饱和激活函数和He初始化可以在训练开始减小梯度消失和梯度爆炸问题，但是不能保证训练过程中不会出现
Batch Normalization用来缓解梯度消失和梯度爆炸问题。在训练过程中，由于之前的网络参数改变，每一层的输入分布也改变（Internal Covariate Shift问题）
这种技术主要包括：在每一层的激活函数之前添加一个操作，0中心化和正太化输入，然后缩放和平移。为了0中心化和正太化输入，算法需要估计输入的均值和标准差。实际中，通过估计当前的mini-batch的均值和标准差。其算法如下$$\begin{aligned}\mu_B &= \dfrac{1}{m_B}\sum_{i=1}^{m_B}\mathbf{x}^{(i)}\\\sigma_B ^2 &= \dfrac{1}{m_B}\sum_{i=1}^{m_B}(\mathbf{x}^{(i)}-\mu_B)^2\\\hat{\mathbf{x}}^{(i)} &= \dfrac{\mathbf{x}^{(i)}-\mu_B}{\sqrt{\sigma_B ^2 + \epsilon}}\\\mathbf{z}^{(i)} &= \gamma \hat{\mathbf{x}}^{(i)} + \beta\end{aligned}$$其中\(\mu_B, \sigma_B, m_B\)分别是mini-batch的均值，方差，和样本个数，\(\mathbf{x}^{(i)}\)是0均值和正太化的输入，\(\gamma, \beta\)分别是缩放参数和平移参数，\(\mathbf{z}^{(i)}\)是BN的输出，\(\epsilon\)是为了防止除0操作
在测试阶段，使用整个训练集的均值和方差。在训练阶段，使用移动平均方法计算均值\(\mu\)和方差\(\sigma\)
解决梯度爆炸
- 梯度裁剪
- 迁移学习（重用预训练层）
快速优化算法
本节会介绍：Momentum optimization、Nesterov Accelerated Gradient、AdaGrad、RMSProp和Adam算法
结论：Adam算法应该是第一选择
Momentum optimization
常规的梯度下降算法只考虑当前的梯度，更新公式为\(\theta = \theta - \eta\bigtriangledown_{\theta} J(\theta)\). 其没有考虑之前的梯度，如果局部梯度小，则其更新缓慢。而Momentum optimization考虑之前的梯度，更新公式如下$$\begin{aligned}\mathbf{m} &= \beta\mathbf{m}+\eta\bigtriangledown_{\theta}J(\theta)\\\theta &= \theta - \mathbf{m}\end{aligned}$$其中\(\beta\)可理解为摩擦系数（一般设置为0.9），\(\bigtriangledown_{\theta}J(\theta)\)理解为加速度
优点是学习速度块，可以帮助跳出局部最优值
Nesterov Accelerated Gradient
Nesterov Accelerated Gradient不是在当前位置计算损失函数梯度，而是在动量方向稍微之前的位置计算梯度，即更新公式如下$$\begin{aligned}\mathbf{m} &= \beta\mathbf{m}+\eta\bigtriangledown_{\theta}J(\theta + \beta\mathbf{m})\\\theta &= \theta - \mathbf{m}\end{aligned}$$一般来说，动量向量将一直指向正确的方向（最优解的方向），因此在动量方向稍微之前的位置计算梯度会获得更多的加速，如下图所示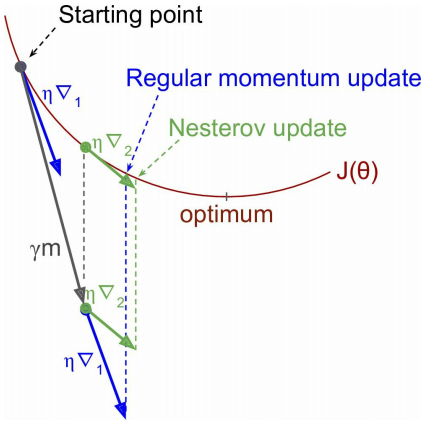
其中\(\bigtriangledown_1\)表示在起始点\(\theta\)的梯度，\(\bigtriangledown_2\)表示在\(\theta + \beta\mathbf{m}\)的梯度
优点是学习速度比Momentum optimization快
AdaGrad
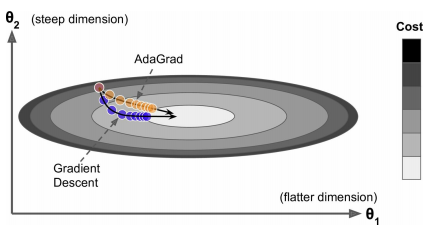对于椭圆形的损失函数，常规的梯度下降算法开始时候沿着梯度最陡的方向下降，之后缓慢移动到最优点（坡度较缓）。如果算法可以提前检测和修正下降的方向，使其朝向全局最优点，将会有助于训练。AdaGrad算法通过缩减沿着最陡方向的梯度实现这一点，其更新公式如下$$\begin{aligned}\mathbf{s} &= \mathbf{s} + \bigtriangledown_{\theta}J(\theta)\otimes\bigtriangledown_{\theta}J(\theta)\\\theta &= \theta - \eta\bigtriangledown_{\theta}J(\theta)\oslash\sqrt{\mathbf{s}+\epsilon}\end{aligned}$$其中\(\otimes\)表示逐元素相乘，\(\oslash\)表示逐元素相除，\(\sqrt{\mathbf{s}+\epsilon}\)理解为学习率衰减，因此，此种方法也称为自适应学习率(adaptive learning rate)
存在问题：AdaGrad对于二次规划问题表现的好，但是对于神经网络，其过早停止（学习率衰减太大）, 不能保证到达全局最优点。因此对于神经网络，不应该使用此优化
RMSProp
RMSProp算法解决了AdaGrad的缺点，RMSProp仅仅累加最近迭代的梯度而不是从开始迭代的梯度（通过指数加权平均实现），其更新公式如下$$\begin{aligned}\mathbf{s} &= \beta\mathbf{s} + (1-\beta)\bigtriangledown_{\theta}J(\theta)\otimes\bigtriangledown_{\theta}J(\theta)\\\theta &= \theta - \eta\bigtriangledown_{\theta}J(\theta)\oslash\sqrt{\mathbf{s}+\epsilon}\end{aligned}$$其表现优于AdaGrad、Momentum optimization和Nesterov Accelerated Gradient优化方法
Adam
Adam组合RMSProp和Momentum optimization，称为adaptive moment estimation（自适应距估计），其更新公式如下$$\begin{aligned}\mathbf{m} &= \beta_1\mathbf{m} + (1-\beta_1)\bigtriangledown_{\theta}J(\theta)\\
\mathbf{s} &= \beta_2\mathbf{s} + (1-\beta_2)\bigtriangledown_{\theta}J(\theta)\otimes\bigtriangledown_{\theta}J(\theta)\\
\mathbf{m} &= \dfrac{\mathbf{m}}{1-\beta_1 ^T}\\
\mathbf{s} &= \dfrac{\mathbf{s}}{1-\beta_2 ^T}\\
\theta &= \theta - \eta\mathbf{m}\oslash\sqrt{\mathbf{s}+\epsilon}
\end{aligned}$$均值称为一阶距，方差称为二阶距，\(T\)表示迭代的次数
其中第3和第4个公式称为偏差修正(\(\mathbf{m}\)和\(\mathbf{s}\)初始化被设为0)，Adam算法也是自适应学习率算法
学习率调度
在训练过程中不断调整学习率，例如设置学习率分段函数，指数衰减等等