约瑟夫环

发表于 | 分类于

题目：已知n个人（以编号0，1，2…n-1分别表示）围坐在一起。从编号为0的人开始报数，数到k的那个人出列；他的下一个人又从1开始报数，数到k的那个人又出列；依此规律重复下去，直到圆桌周围的人全部出列，最后一个出列的人为胜利者。求胜利者编号

递归的方法

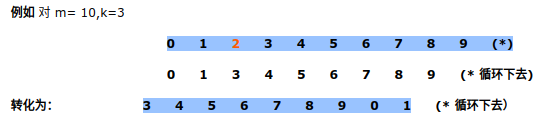示意图当\(m=10, \quad k=3\)去掉一个元素时，变为一个\(m=9, \quad k=3\)的约瑟夫环问题，且有如下关系$$3 = (0 + 3) \% 10 \quad 4 = (1 + 3) \% 10 \dots 1 = (8 + 3) \% 10 \\\Downarrow \\3 = (0 + k) \% m \quad 4 = (1 + k) \% m \dots 1 = (8 + k) \% m$$当\(m = 10, \quad k=3\)时，设约瑟夫环最后一个出列的人为\(\text{Joseph}(10, 3)\)，则有如下关系$$\text{Joseph}(10, 3) = (\text{Joseph}(9, 3) + k) \% m\\\vdots \\ \text{Joseph}(2, 3) = (\text{Joseph}(1, 3) + k) \% m$$C++实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <iostream>
#include <vector>
using namespace std;

int josephLoop(int m, int k)
{
    if(m <= 0 || k <= 0) return -1;
    if(m == 1) return 0;
    return (josephLoop(m-1, k) + k) % m;
}
int main(int argc, char* argv[])
{
    int m = 10, k = 3;
    cout << josephLoop(m, k) << endl;
    return 0;
}

输出结果：3
输出整个出队顺序的C++实现为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream>
#include <vector>
using namespace std;

int josephLoop_res(int m, int k, int i)
{
    if(m <= 0 || k <= 0) return -1;
    if(i == 1) return (m + k - 1) % m;
    return (josephLoop_res(m-1, k, i-1) + k) % m;
}

int main(int argc, char* argv[])
{
    int m = 10, k = 3;
    cout << "出队序列：" << endl;
    for(int i = 1; i <= m; ++i)
        cout << josephLoop_res(m, k, i) << " ";
    cout << endl;
    return 0;
}

输出结果：2 5 8 1 6 0 7 4 9 3

循环链表实现

C++实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <iostream>
using namespace std;

struct Node
{
    int val;
    Node* next;
    Node(int n): val(n), next(nullptr){}
};

void josephus(int m, int k)
{
    // creat loop list
    if(k < 2) return;
    Node* pHead = new Node(0);
    Node* currentNode = pHead;
    for(int i = 1; i < m; ++i)
    {
        Node* tmpNode = new Node(i);
        currentNode->next = tmpNode;
        currentNode = tmpNode;
    }
    currentNode->next = pHead; // 尾节点和首节点相连接
    Node* pTail = currentNode;
    // 模拟约瑟夫环问题，删除节点
    for(int i = 0; i < m-1; ++i)
    {
        int k_tmp = k;
        Node* parentNode = nullptr;
        Node* gNode = nullptr; // 祖父节点
        while(k_tmp > 0)
        {
            gNode = parentNode;
            parentNode = pHead;
            pHead = pHead->next;
            k_tmp--;
        }
        gNode->next = pHead;
        cout << parentNode->val << " ";
    }
    cout << pHead->val << endl;
}
int main()
{
    int m = 10, k = 3;
    if(k == 1) return m-1;
    josephus(m, k);
    return 0;
}

输出结果：2 5 8 1 6 0 7 4 9 3